0 445416 445424 445430 445434 445440 445442 445446 445452 445454 445460 445466 445470 445472 445476 445482 445484 445490 445494 445496 445500 445502 445506 445508 445510 445511 445512 445514 445515 445516 445518 445520 445524 445526 445530 445532 445536 445542 445544 445550 445554 445556 445560 445566 445572 445574 445580 445584 445586 445592 445596 445602 445610 447348
 的单调递增区间为 ( )
的单调递增区间为 ( )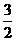 ) D.(
) D.(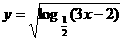 的定义域是 ( )
的定义域是 ( )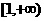 B.
B.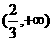 C.
C.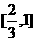 D.
D.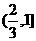
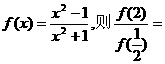 ( )
( )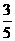 D.
D.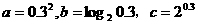 之间的大小关系是 ( )
之间的大小关系是 ( )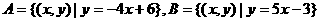 ,则
,则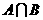 = ( )
= ( )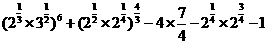
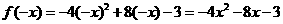 ∵f(x)是偶函数,
∵f(x)是偶函数,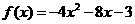
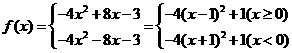
 和[0,1]
和[0,1]
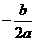 =2即b= - 4a
=2即b= - 4a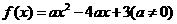
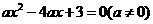 的两个实根为 x1,x2,
的两个实根为 x1,x2,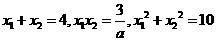
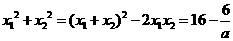 ,所以
,所以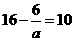
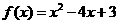
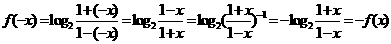
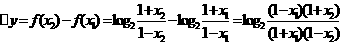
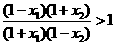
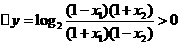
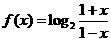 在(- 1,1)上是增函数
在(- 1,1)上是增函数 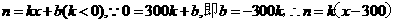
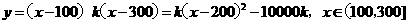

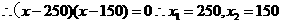
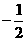 ,
,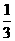 }
}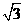 (16)
②③④
(16)
②③④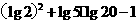 (Ⅱ)
(Ⅱ) 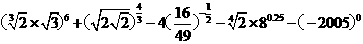
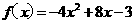 .
.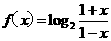 ,(x∈(- 1,1).
,(x∈(- 1,1).