3.球的表面积公式和体积公式:设球的半径为R,则球的表面积S= ;球的体积V= .
|
例1. 如图,A、B、C是半径为1的球面上的三点,B、C两点间的球面距离为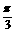 ,点A与B、C两点的球面距离都为
,点A与B、C两点的球面距离都为 ,O为球心,求:
,O为球心,求:
(1)  的大小;
的大小;
(2) 球心O到截面ABC的距离.

解:(1) 因为B、C两点的球面距离为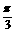 ,即B、C两点与球心连线所夹圆心角为
,即B、C两点与球心连线所夹圆心角为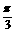 ,点A与B、C两点的球面距离都为
,点A与B、C两点的球面距离都为 ,即
,即 均为直角,所以
均为直角,所以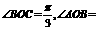

(2) 因为⊿BOC,⊿ABC都是等腰三角形,取BC的中点M,连OM,AM,过O作OH⊥AM于H,可证得OH即为O到截面ABC的距离.

变式训练1: 球面上有三点A、B、C,A和B及A和C之间的球面距离是大圆周长的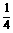 ,B和C之间的球面距离是大圆周长的
,B和C之间的球面距离是大圆周长的 ,且球心到截面ABC的距离是
,且球心到截面ABC的距离是 ,求球的体积.
,求球的体积.
解:设球心为O,由已知,易得∠AOB=∠AOC= ,∠BOC=
,∠BOC=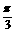 ,过O作OD⊥BC于D,连AD,再过O作OE⊥AD于E,则OE⊥平面ABC于E,∴OE=
,过O作OD⊥BC于D,连AD,再过O作OE⊥AD于E,则OE⊥平面ABC于E,∴OE= . 在Rt△AOD中,由AD·OE=AO·OD
. 在Rt△AOD中,由AD·OE=AO·OD OA=R=1.∴ V球=
OA=R=1.∴ V球= πR3=
πR3= π.
π.
例2. 如图,四棱锥A-BCDE中, ,且AC⊥BC,AE⊥BE.
,且AC⊥BC,AE⊥BE.
(1) 求证:A、B、C、D、E五点都在以AB为直径的同一球面上;
(2) 若 求B、D两点间的球面距离.
求B、D两点间的球面距离.

解:(1) 因为AD⊥底面BCDE,所以AD⊥BC,AD⊥BE,又因为AC⊥BC,AE⊥BE,所以BC⊥CD,BE⊥ED.故B、C、D、E四点共圆,BD为此圆的直径.
取BD的中点M,AB的中点N,连接BD、AB的中点MN,则MN∥AD,所以MN⊥底面BCDE,即N的射影是圆的圆心M,有AM=BM=CM=DM=EM,故五点共球且直径为AB.
(2) 若∠CBE=90°,则底面四边形BCDE是一个矩形,连接DN,因为:

所以B、D两点间的球面距离是 .
.
变式训练2:过半径为R的球面上一点M作三条两两互相垂直的弦MA、MB、MC.
(1) 求证:MA2+MB2+MC2为定值;
(2) 求△MAB,△MAC,△MBC面积之和的最大值.
解:(1) 易求得MA2+MB2+MC2=4R2!
(2)
S△MAB+S△MAC+S△MBC= (MA·MB+MA·MC+MB·MC)≤
(MA·MB+MA·MC+MB·MC)≤ (MA2+MB2+MC2)=2R2(当且仅当MA=MB=MC时取最大值).
(MA2+MB2+MC2)=2R2(当且仅当MA=MB=MC时取最大值).
例3.棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面(如图),则图中三角形(正四面体的截面)的面积是( )
 A.
A.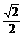
B.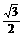
C.
D.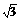
解:设正四面体为正四面体ABCD,分析截面图可知,截面经过正四面体的一条棱设为CD,又过球心,设截面与棱AB交于E点,则E为AB的中点,易求得截面三角形的面积为 ,
,
故选(C).
变式训练3:已知三棱锥P-ABC中,E、F分别是AC、AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.
(1) 证明:PC⊥平面PAB;
(2) 求二面角P-AB-C的平面角的余弦值;
(3) 若点P、A、B、C在一个表面积为12π的球面上,求△ABC的边长.
解 (1) 连结CF,∵PE=EF= BC=
BC= AC ∴AP⊥PC ∵CF⊥AB, PF⊥AB, ∴AB⊥平面PCF ∵AC
AC ∴AP⊥PC ∵CF⊥AB, PF⊥AB, ∴AB⊥平面PCF ∵AC 平面PCF ∴PC⊥AB ∴PC⊥平面PAB.
平面PCF ∴PC⊥AB ∴PC⊥平面PAB.
(2) ∵AB⊥PF, AB⊥CF ∴∠PFC为所求二面角的平面角
设AB=a, 则PF=EF= , CF=
, CF= ,
,
∴cos∠PFC= .
.
(3) 设PA=x, 球半径为R
∵PC⊥平面PAB,PA⊥PB
∵4πR2=12π,
∴R=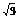 , 知△ ABC的外接圆为球之小圆,由x2=
, 知△ ABC的外接圆为球之小圆,由x2= x·2R.
x·2R.
得△ABC的边长为2 .
.
|
3.在解正棱锥问题时,要注意利用四个直角三角形,其中分别含有九个元素(侧棱、高、侧棱与斜高在底面上的射影、侧棱与侧面与底面所成角、边心距以及底面边的一半)中的三个,已知两个可求另一个.
第11课时 球
|

4.正棱锥的性质:
① 正棱锥各侧棱 ,各侧面都是 的等腰三角形,各等腰三角形底边上的高 (它叫做正棱锥的 );
② 正棱锥的高、斜高和斜高在底面内的射影组成一个 三角形,正棱锥的高、侧棱、侧棱在底面内的射影组成一个 三角形.
 |
|||
|
|||
例1.已知正四棱柱ABCD-A1B1C1D1,AB=1,AA1=2,
点E为CC1的中点,点F为BD1的中点.
⑴ 证明:EF为BD1与CC1的公垂线;
⑵ 求点F到面BDE的距离.
答案(1)略; (2) 
 变式训练1:三棱柱ABC-A1B1C1中,AB=
变式训练1:三棱柱ABC-A1B1C1中,AB= a,
a,
BC、AC、AA1长均为a,A1在底面ABC上的射影O在AC上.
⑴ 求AB与侧面AC1所成的角;
⑵ 若O点恰是AC的中点,求此三棱柱的侧面积.
 答案(1)
45°;(2)
答案(1)
45°;(2) 
例2. 如图,正三棱锥P-ABC中,侧棱PA与底面ABC成60°角.
(1)求侧PAB与底面ABC成角大小;
(2)若E为PC中点,求AE与BC所成的角;
(3)设AB= ,求P到面ABC的距离.
,求P到面ABC的距离.
解:(1) ;
;
(2)取PB中点F,连结EF,则∠AEF为所求的角,求得∠AEF= ;
;
 (3)P到平面ABC的距离为
(3)P到平面ABC的距离为 .
.
变式训练2: 四面体ABCD中,O、E分别是BD、BC的中点,
CA=CB=CD=BD=2,AB=AD= .
.
(1)求证:AO⊥平面BCD;
(2)求异面直线AB与CD所成的角;
(3)求点E到平面ACD的距离.
答案:(1)易证AO⊥BD,AO⊥OC,∴AO⊥平面BCD;
(2) ;(3)用等体积法或向量法可求得点E到平面ACD的距离是
;(3)用等体积法或向量法可求得点E到平面ACD的距离是 .
.
 例3. 四棱锥P-ABCD的底面ABCD是直角梯形,AB∥CD,AB=2,CD=1,∠DAB=45°;侧面PAD是等腰直角三角形,AP=PD,且平面PAD⊥平面ABCD.
例3. 四棱锥P-ABCD的底面ABCD是直角梯形,AB∥CD,AB=2,CD=1,∠DAB=45°;侧面PAD是等腰直角三角形,AP=PD,且平面PAD⊥平面ABCD.
⑴ 求证:PA⊥BD;
⑵ 求PB与底面ABCD所成角的正切值;
⑶ 求直线PD与BC所成的角.
答案:(1)略;(2) ;(3)60°
;(3)60°
变式训练3:在所有棱长均为a的正三棱柱ABC-A1B1C1中,D为BC的中点.
 ⑴ 求证:AD⊥BC1;
⑴ 求证:AD⊥BC1;
⑵ 求二面角A-BC1-D的大小;
⑶ 求点C到平面ABC1的距离.
提示:(1)证AD⊥平面BB1C1C;(2)
arc tan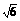 ;(3)
;(3)  a.
a.
 例4.如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=1,M为AB的中点,A1D=3DB1.
例4.如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=1,M为AB的中点,A1D=3DB1.
(1)求证:平面CMD⊥平面ABB1A1;
(2)求点A1到平面CMD的距离;
(3)求MD与B1C1所成角的大小.
提示(1)转证CM⊥平面A1B;
(2)过A1作A1E⊥DM,易知A1E⊥平面CMD,∴求得A1E=1;
(3)异面直线MD与B1C1所成的角为
变式训练4:在长方体ABCD-A1B1C1D1中,AA1=AD=1,AB= ,O为对角线A1C的中点.
,O为对角线A1C的中点.
⑴ 求OD与底面ABCD所成的角的大小;
⑵ P为AB上一动点,当P在何处时,平面POD⊥平面A1CD?并证明你的结论.
答案(1) 30°;(2) 当P为AB的中点时,平面POD⊥平面A1CD.
|
柱体和锥体是高考立体几何命题的重要载体,因此,在学习时要注意以下三点.

 与球半径
与球半径 及截面的半径
及截面的半径 有以下关系:
.
有以下关系:
.