摘要：20． 已知椭圆C:+＝1的离心率为.过右焦点F且斜率为1的直线交椭圆C于A.B两点.N为弦AB的中点. 1)求直线ON(O为坐标原点)的斜率KON , 2)对于椭圆C上任意一点M .试证:总存在角(∈R)使等式:＝cos+sin成立.
网址：http://m.1010jiajiao.com/timu3_id_4454433[举报]
（本小题满分13分）
已知过椭圆C：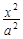
＋
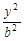＝1（a＞b＞0）右焦点F且斜率为1的直线交椭圆C于A，B两点，N为弦AB的中点；又函数
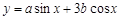图象的一条对称轴的方程是
.
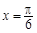（1）求椭圆C的离心率e与直线AB的方程；
（2）对于任意一点M∈C，试证：总存在角θ（θ∈R）使等式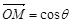
+
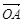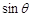
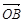成立.
查看习题详情和答案>>
（本小题满分13分）
如图所示，椭圆C：
的一个焦点为 F(1,0)，且过点
。
(1)求椭圆C的方程;
(2)已知A、B为椭圆上的点，且直线AB垂直于
轴，
直线
：＝4与轴交于点N，直线AF与BN交
于点M。
(ⅰ)求证：点M恒在椭圆C上；
(ⅱ)求△AMN面积的最大值．
查看习题详情和答案>>
如图所示，椭圆C：
的一个焦点为 F(1,0)，且过点
。
轴， 
：
＋
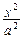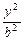＝1（a＞b＞0）右焦点F且斜率为1的直线交椭圆C于A，B两点，N为弦AB的中点；又函数
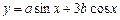图象的一条对称轴的方程是
.
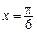C
+
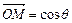
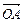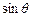
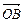成立.