0 445213 445221 445227 445231 445237 445239 445243 445249 445251 445257 445263 445267 445269 445273 445279 445281 445287 445291 445293 445297 445299 445303 445305 445307 445308 445309 445311 445312 445313 445315 445317 445321 445323 445327 445329 445333 445339 445341 445347 445351 445353 445357 445363 445369 445371 445377 445381 445383 445389 445393 445399 445407 447348

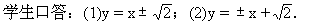
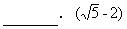
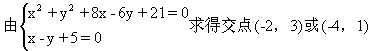
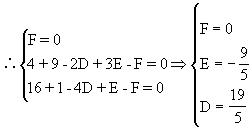
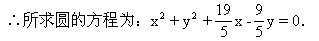
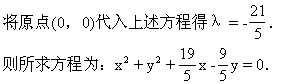
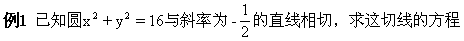

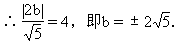

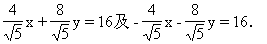
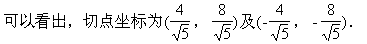
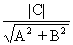
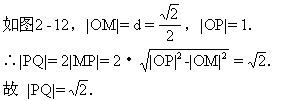
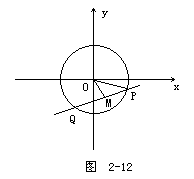
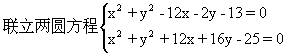

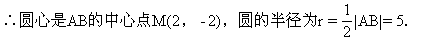
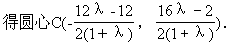
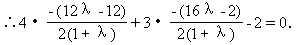
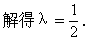
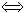 点M在圆外;
点M在圆外;