0 152482 152490 152496 152500 152506 152508 152512 152518 152520 152526 152532 152536 152538 152542 152548 152550 152556 152560 152562 152566 152568 152572 152574 152576 152577 152578 152580 152581 152582 152584 152586 152590 152592 152596 152598 152602 152608 152610 152616 152620 152622 152626 152632 152638 152640 152646 152650 152652 152658 152662 152668 152676 447348
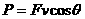 求功率要注意
求功率要注意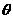 角的意义,它是指力
角的意义,它是指力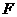 与速度
与速度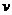 间的夹角。
间的夹角。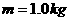 的物体以初速度
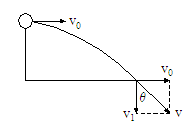
的物体以初速度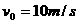 做平抛运动。则在第1.0s末重力的瞬时功率为多大?(
做平抛运动。则在第1.0s末重力的瞬时功率为多大?(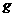 取
取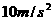 )
)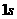 末物体的竖直分速度为
末物体的竖直分速度为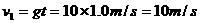
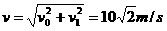
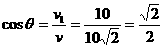
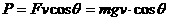
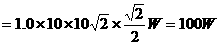
 的物体,在几个共点力的作用下静止在光滑的水平桌面上,现把其中一个水平方向的力F突然增大到3F,保持其他力不变,则在
的物体,在几个共点力的作用下静止在光滑的水平桌面上,现把其中一个水平方向的力F突然增大到3F,保持其他力不变,则在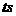 末该力的功率为( )
末该力的功率为( ) 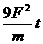 B.
B. 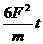 C.
C. 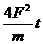 D.
D. 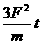
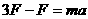
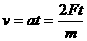
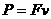 得
得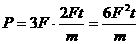
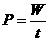 计算;其二,用推导式
计算;其二,用推导式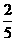 ,则该运动员跳绳时克服重力做功的平均功率为多大?(
,则该运动员跳绳时克服重力做功的平均功率为多大?(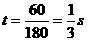
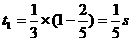
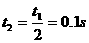
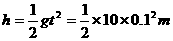
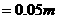
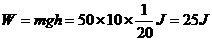
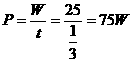 。
。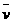 ,由运动学公式得
,由运动学公式得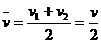 ,则力F在这段时间内的平均功率为
,则力F在这段时间内的平均功率为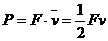 。
。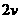 的速率匀速行驶时,汽车发动机的功率为( )
的速率匀速行驶时,汽车发动机的功率为( ) 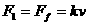 ,此时汽车的功率为
,此时汽车的功率为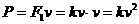 ①
①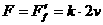 ,此时汽车的功率变为
,此时汽车的功率变为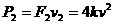 ②
②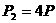
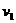
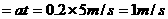
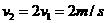 ,所以在第5s末力F的功率为
,所以在第5s末力F的功率为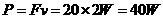 。
。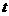 内的平均功率。功率的推导式为
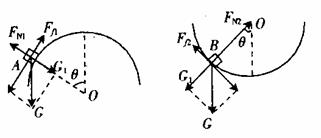
内的平均功率。功率的推导式为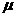 ,试分别求出木块沿竖直圆轨道外侧滑到A点和沿圆轨道内侧滑到B点时受到的摩擦力大小(设圆轨道半径为R,滑到A点到B点的速度均为
,试分别求出木块沿竖直圆轨道外侧滑到A点和沿圆轨道内侧滑到B点时受到的摩擦力大小(设圆轨道半径为R,滑到A点到B点的速度均为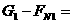
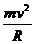
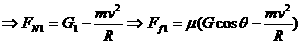 ,当木块滑到圆轨道内侧B点时,受力分析如图4-乙所示,则有
,当木块滑到圆轨道内侧B点时,受力分析如图4-乙所示,则有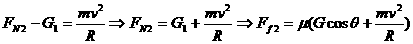 。
。
 从A滑到B时速度变为
从A滑到B时速度变为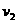 ,则
,则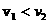 B.
B. 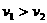 C.
C. 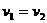 D. 无法判定
D. 无法判定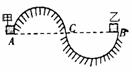
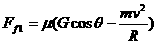 ,即
,即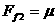
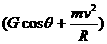 。即
。即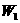 ;若该物体从
;若该物体从 沿两斜面滑到
沿两斜面滑到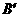 ,物体克服摩擦力做的总功为
,物体克服摩擦力做的总功为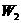 ,如图2所示,已知物体与各接触面间的动摩擦因数均相同,则( )
,如图2所示,已知物体与各接触面间的动摩擦因数均相同,则( )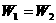 B.
B. 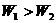 C.
C.  D. 无法确定
D. 无法确定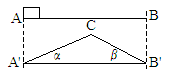
 。则从A到B过程中,物体克服摩擦力做的功为
。则从A到B过程中,物体克服摩擦力做的功为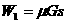 。
。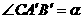 ,
,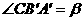 ),物体克服摩擦力做的功为
),物体克服摩擦力做的功为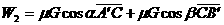
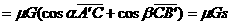
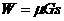 (
(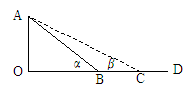
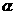 、
、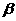 。物体沿DBA滑动时,合力做功
。物体沿DBA滑动时,合力做功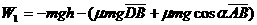
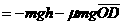 。同法可得当物体沿DCA滑动时,合力做功为
。同法可得当物体沿DCA滑动时,合力做功为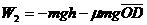 ,即两次合力做功相等,根据动能定理
,即两次合力做功相等,根据动能定理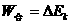 可得,两次物体动能变化也相等,因此当物体沿DCA滑到顶端速度为零时,物体具有的初速度也等于
可得,两次物体动能变化也相等,因此当物体沿DCA滑到顶端速度为零时,物体具有的初速度也等于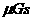 (
(
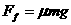 不变,而方向时刻改变,是变力,但若把圆周分成无数小微元段,则每一小段可认为摩擦力方向不变,每一小段可用恒力做功公式计算,然后各段求和便得。
不变,而方向时刻改变,是变力,但若把圆周分成无数小微元段,则每一小段可认为摩擦力方向不变,每一小段可用恒力做功公式计算,然后各段求和便得。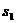 、
、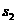 、
、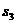 ……
……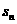 ,摩擦力在每一段做功分别为
,摩擦力在每一段做功分别为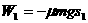 、
、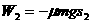 ……
……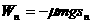 ,则摩擦力在一周内所做的功
,则摩擦力在一周内所做的功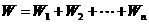
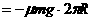 。
。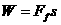 (
(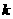 倍,而小球与地面相碰后能以相同大小的速率反弹,求小球从释放至停止所通过的总路程。
倍,而小球与地面相碰后能以相同大小的速率反弹,求小球从释放至停止所通过的总路程。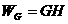 (重力做功与路径无关)。
(重力做功与路径无关)。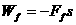 (
(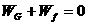 ,即
,即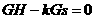
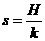
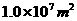 ,涨潮时水深
,涨潮时水深 ,此时关上水坝闸门,可使水位保持
,此时关上水坝闸门,可使水位保持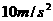 (不考虑浮力作用)
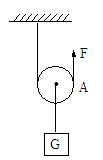
(不考虑浮力作用)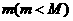 的物体B相连,系统由静止开始运动,当A的速度为v时,牵引它的绳子与水平方向成
的物体B相连,系统由静止开始运动,当A的速度为v时,牵引它的绳子与水平方向成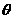 角,不计滑轮与绳子的质量和摩擦,求此运动过程中物体B的重力做了多少功?
角,不计滑轮与绳子的质量和摩擦,求此运动过程中物体B的重力做了多少功?