0 152487 152495 152501 152505 152511 152513 152517 152523 152525 152531 152537 152541 152543 152547 152553 152555 152561 152565 152567 152571 152573 152577 152579 152581 152582 152583 152585 152586 152587 152589 152591 152595 152597 152601 152603 152607 152613 152615 152621 152625 152627 152631 152637 152643 152645 152651 152655 152657 152663 152667 152673 152681 447348
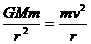 ,得
,得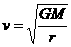
 越大,
越大,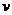 越小;
越小;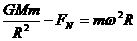 ,这里
,这里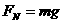
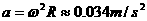 ,远远小于地面上的重力加速度
,远远小于地面上的重力加速度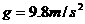 ,在近似计算中可忽略自转的影响,认为地面上物体的重力等于万有引力。
,在近似计算中可忽略自转的影响,认为地面上物体的重力等于万有引力。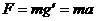 。卫星的向心加速度
。卫星的向心加速度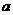 等于卫星所在处的重力加速度
等于卫星所在处的重力加速度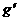 。对近地卫星,有
。对近地卫星,有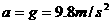 。
。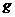 ,物体在赤道上随地球自转的向心加速度为
,物体在赤道上随地球自转的向心加速度为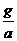 倍 B.
倍 B. 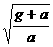 倍 C.
倍 C. 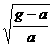 倍 D.
倍 D. 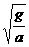 倍
倍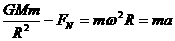 ,其中
,其中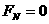 ,于是
,于是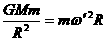
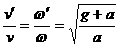 ,选项B正确。
,选项B正确。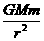
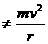 ,运行轨道发生变化。若
,运行轨道发生变化。若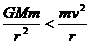 ,卫星做离心运动;若
,卫星做离心运动;若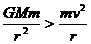 ,卫星做近心运动。
,卫星做近心运动。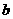 、
、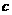 是三颗在圆轨道上运行的卫星,则( )
是三颗在圆轨道上运行的卫星,则( )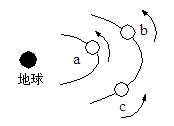
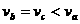 ,故A错。
,故A错。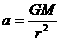 知,
知,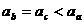 ,故B错。
,故B错。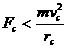 ,它将偏离原轨道,做离心运动;当
,它将偏离原轨道,做离心运动;当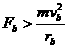 ,它将偏离原轨道,做近心运动。所以C错。
,它将偏离原轨道,做近心运动。所以C错。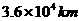 处,线速度为
处,线速度为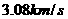 。
。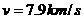 ,最小周期大约84min(近地卫星)。
,最小周期大约84min(近地卫星)。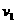 ,加速度为
,加速度为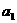 ,地球赤道上的物体随地球自转的向心加速度为
,地球赤道上的物体随地球自转的向心加速度为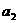 ,第一宇宙速度为
,第一宇宙速度为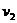 ,地球半径为R,则( )
,地球半径为R,则( ) 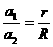 B.
B. 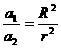 C.
C. 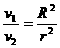 D.
D. 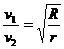
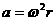 知
知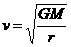 ,所以
,所以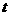 ,地球同步卫星的高度为
,地球同步卫星的高度为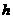 ,地球的公转周期为T,自转周期为
,地球的公转周期为T,自转周期为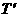 。地球半径为R。试推导太阳和地球的质量的表达式。
。地球半径为R。试推导太阳和地球的质量的表达式。 ,则
,则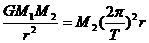 ,而
,而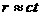 (
(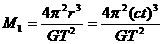
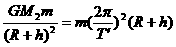
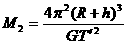
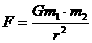 中的
中的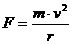 中的
中的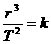 中的
中的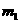 和
和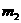 ,相距为
,相距为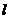 ,万有引力常量为G,求:
,万有引力常量为G,求: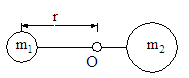
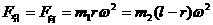
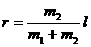
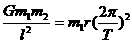
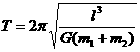
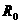 )
)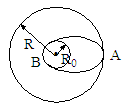
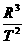
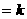 ,当飞船进入椭圆轨道运动时,有
,当飞船进入椭圆轨道运动时,有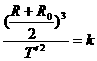 ,由两式联立得飞船在椭圆轨道上运动的周期
,由两式联立得飞船在椭圆轨道上运动的周期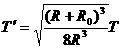 ,故解得飞船由A运动到B点所需的时间为
,故解得飞船由A运动到B点所需的时间为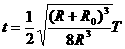 。
。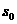 ,有
,有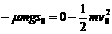 (4分) 得
(4分) 得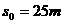 (2分)
(2分) 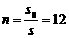 (个) (3分)
(个) (3分)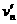
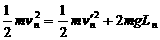 ① (2分)
① (2分)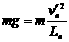 ② (2分)
② (2分) 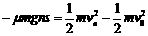 ③(3分)
③(3分)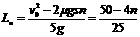 (4分)
(4分)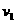 ,则有
,则有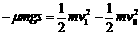 由于滑块与小球碰撞时不损失机械能,则碰撞前后动能相等,滑块与小球相碰撞会互换速度,碰撞后瞬间小球的速度仍为
由于滑块与小球碰撞时不损失机械能,则碰撞前后动能相等,滑块与小球相碰撞会互换速度,碰撞后瞬间小球的速度仍为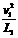
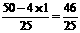 由上述三式解得:T=0.6N
由上述三式解得:T=0.6N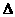 E=mg(x1+x2)-m1g(x1+x2)--(3)(3分)
E=mg(x1+x2)-m1g(x1+x2)--(3)(3分)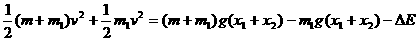 ----(4)(3分)
----(4)(3分)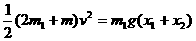 -----(5)(2分)
-----(5)(2分)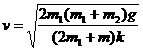 -----------------(6)(2分)
-----------------(6)(2分)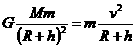 , ①(2分)
, ①(2分)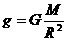 ②(2分)
②(2分)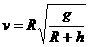 (2分)
(2分)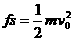 ③(3分)
③(3分)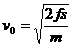 (1分)
(1分)