4.用平行于斜面向下的拉力F将一个物体沿斜面往下拉动后，拉力的大小等于摩擦力，则

A.物体做匀速运动

B.合外力对物体做功等于零

C.物体的机械能减少

D.物体的机械能不变

解析：物体所受的力中，重力、拉力、摩擦力对物体做功，拉力与摩擦力做的功相互抵消，重力做功不影响机械能，故物体的机械能不变.

答案：D

3.如图所示，长为L的轻杆一段固定一质量为m的小球，另一端安装有固定转动轴O，杆可在竖直平面内绕O无摩擦转动.若在最低点P处给小球一沿切线方向的初速度v₀＝2，不计空气阻力，则下列说法正确的是(　)

A.小球不可能到达圆周轨道的最高点Q

B.小球能达到圆周轨道的最高点Q，且在Q点受到轻杆向上的支持力

C.小球能到达圆周轨道的最高点Q，且在Q点受到轻杆向下的拉力

D.小球能达到圆周轨道的最高点Q，且在Q点恰好不受轻杆的弹力

解析：设小球能到达Q点，且到达Q点时具有速度v，由机械能守恒得：

mv＝mg·2L+mv²

可解得：v＝0

在最高点，小球所需的向心力为零，故受轻杆向上的大小为mg的支持力.

答案：B

2.如图所示，在地面上以速度v₀抛出质量为m的物体，抛出后物体落到比地面低h的海平面上.若以地面为零势能面且不计空气阻力，则下列说法中不正确的是(　)

A.物体到海平面时的重力势能为mgh

B.重力对物体做的功为mgh

C.物体在海平面上的动能为mv+mgh

D.物体在海平面上的机械能为mv

解析：以地面为参考平面，物体在海平面时的重力势能为－mgh，故A错误；抛出后的过程中机械能守恒，所以C、D正确；重力做功与路径无关，所以B正确.

答案：A

1.质量为m的物体由静止开始以2g的加速度竖直向下运动h高度.下列说法中正确的是(　)

A.物体的势能减少2mgh　B.物体的机械能保持不变

C.物体的动能增加2mgh　 D.物体的机械能增加mgh

解析：重力势能的减少量等于重力做的功，即ΔE_p＝mgh，A错误.

由题意知，物体除受重力外还受大小为mg的向下的作用力，机械能不守恒，B错误.

物体的合外力F_合＝2mg，故其动能的增量ΔE_k＝2mgh，C正确.

ΔE_p＝－mgh，ΔE_k＝2mgh，故ΔE＝ΔE_k+ΔE_p＝mgh，D正确.

答案：CD

10.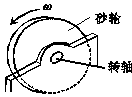(12分)探究能力是物理学研究的重要能力之一. 物体因绕轴转动而具有的动能叫转动动能，转动动能的大小与物体转动的角速度有关.为了研究某一砂轮的转动动能E_k与角速度ω的关系，某同学采用了下述实验方法进行探索：先让砂轮由动力带动匀速旋转测得其角速度ω，然后让砂轮脱离动力，由于克服转轴间的摩擦力做功，砂轮最后停下，测出砂轮脱离动力到停止转动的圈数n，通过分析实验数据，得出结论.经实验测得的几组ω和n的数据如下表所示，另外已测得砂轮转轴的直径D＝1 cm，转轴间的摩擦力为 N.

(1)计算出砂轮每次脱离动力的转动动能，并填入表格中.

(2)由上述数据推导出该砂轮的转动动能E_k与角速度ω的关系式为：　　　　.

(3)若测得脱离动力后砂轮的角速度为2.5 rad/s，则它转过45圈时的角速度为　　　rad/s.

解析：(1)由能量守恒定律可知，脱离动力时刻砂轮的转动动能等于停止前克服滑动摩擦力做的功，即：

ΔE_k＝W_f＝nπD·f.

(2)由表中数据可得E_k∝ω²，设E_k＝kω²

当有ω＝0.5 rad/s时有：

k×0.5²＝5π×10^－2×

解得：k＝2，故E_k＝2ω².

(3)由动能定理得：E_k′－E_k＝－f·45·πD

解得：E_k′＝2×2.5² J－×45×π×1×10^－2 J＝8 J

又由E_k′＝2ω′²

解得：ω′＝2 rad/s.

答案：(1)0.5　2.0　8.0　18.0　32.0　(2)E_k＝2ω²

(3)2.0

9.(12分)如图所示，将轻弹簧放在凹形光滑轨道上，并将其一端与轨道的相应端固定，轨道放在水平桌面的边缘上，桌边悬一重物.利用该装置可以找出弹簧压缩时具有的弹性势能与压缩量之间的关系.

(1)为完成实验，还需要哪些器材？

答：　　　　　　　　　　　.

(2)如果在实验中，得到弹簧的压缩量x和小球离开桌面后落地的水平位移s的一些数据如下表所示，则得到的实验结论是：　　　　　　　　　　　.

解析：(2)由机械能守恒定律得：E_p＝mv

又由平抛运动的规律知：v₀＝s

可得：本实验中弹簧的弹性势能E_p∝s²

又由实验数据可得：s∝x

可得实验结论：E_p∝x².

　答案：(1)白纸、复写纸、刻度尺

(2)弹簧的弹性势能与弹簧压缩量的平方成正比

8.(12分)某同学利用透明直尺和光电计时器来验证机械能守恒定律，实验的简易示意图如图所示.当有不透光物体从光电门间通过时，光电计时器就可以显示物体的挡光时间.所用的西瓯XDS－007光电门传感器可测得最短时间为0.01 ms.将挡光效果好、宽度d＝3.8×10^－3 m的黑色磁带贴在透明直尺上.现将直尺从一定高度由静止释放，并使其竖直通过光电门.某同学测得各段黑色磁带通过光电门的时间Δt_i与图中所示的高度差Δh_i，并将部分数据进行了处理，结果如下表所示.(取g＝9.8 m/s²，表格中M为直尺的质量)

(1)从表格中的数据可知，直尺上磁带通过光电门的瞬时速度是利用v_i＝求出的，请你简要分析该同学这样做的理由是：　　　　　　　　　　　　.

(2)请将表格中的数据填写完整.

(3)通过实验得出的结论是：　　　　　　　　　　　.

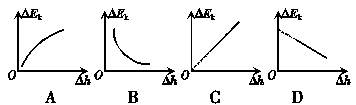
(4)根据该实验，请你判断下列ΔE_k－Δh图象中正确的是(　)

答案：(1)极短时间或极短位移内的平均速度趋近于瞬时速度

(2)4.22　4.00M或4.01M　4.01M或4.02M

(3)在误差允许的范围内，机械能守恒

(4)C

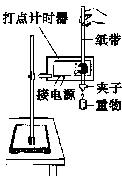7.(12分)用如图甲所示的实验装置验证机械能守恒定律.实验所用的电源为学生电源，输出电压为6 V的交流电和直流电两种.重物从高处由静止开始下落，重物上拖着的纸带打出一系列的点，对纸带上的点痕进行测量，即可验证机械能守恒定律.

(1)下面列举了该实验的几个操作步骤：

A.按照图示的装置安装器件

B.将打点计时器接到电源的“直流输出”上　　　　　　　　　 　　　　　　　

C.用天平测出重物的质量

D.释放悬挂纸带的夹子，同时接通电源开关打出一条纸带

E.测量纸带上某些点间的距离

F.根据测量的结果计算重物下落过程中减少的重力势能是否等于增加的动能

指出其中没有必要进行的或者操作不当的步骤，将其选项对应的字母填在下面的空行内，并说明其原因.

答：　　　　　　　　　　　　　　　　　　.

(2)利用这个装置也可以测量重物下落的加速度a的数值.如图乙所示，根据打出的纸带，选取纸带上的连续的五个点A、B、C、D、E，测出A距起始点O的距离为s₀，点A、C间的距离为s₁，点C、E间的距离为s₂，使用交流电的频率为f，根据这些条件计算重物下落的加速度a＝　　　　.

乙

(3)在“验证机械能守恒定律”的实验中发现，重物减少的重力势能总是大于重物增加的动能，其原因主要是在重物下落的过程中存在阻力作用.可以通过该实验装置测阻力的大小，若已知当地的重力加速度为g，还需要测量的物理量是　　　.试用这些物理量和纸带上的数据符号表示出重物在下落过程中受到的平均阻力大小F＝　　　　.

答案：(1)步骤B是错误的，应该接到电源的交流输出端.步骤D是错误的，应该先接通电源，待打点稳定后再释放纸带.步骤C是不必要的，因为根据测量原理，重物的动能和势能中都包含了质量m，可以约去.

(2)

(3)重物的质量m　m[g－]

6.(12分)在做“利用重物自由下落验证机械能守恒定律”的实验时，某同学按照正确的操作所选的纸带如图所示，其中O点是起始点，A、B、C是打点计时器连续打下的3个点.该同学用毫米刻度尺测量O点到A、B、C各点的距离，并记录在图中.已知电源的频率是 50 Hz.

(1)这三个数据中，不符合有效数字读数要求的测量段是　　　段，应记作　　　cm.

(2)该同学用重物在OB段的运动来验证机械能守恒定律，已知当地的重力加速度g＝9.80 m/s²，他用AC段的平均速度作为跟B点对应的物体的瞬时速度，则该段重物的重力势能的减少量为　　，而动能的增加量为　　(结果均保留三位有效数字，重物的质量用m表示).这样验证的系统误差总是使重力势能的减少量　　　动能的增加量，原因是　　　　　　　　　　　　　　　　　　　　　　　　　.

(3)另一位同学根据同一条纸带、同一组数据，也用重物在OB段的运动来验证机械能守恒.不过他从打点计时器打下的第一个点O数起，图中的B是打点计时器打下的第9个点.因此他用v_B＝gt来计算与B点对应的重物的瞬时速度，得到动能的增加量为　　(结果保留三位有效数字，重物的质量用m表示)，这样验证的系统误差总是使重力势能的减少量　　动能的增加量，原因是　　　　　　

　　　　　　　　　　　　　.

解析：(1)题中是用最小刻度是毫米的刻度尺测量，以cm为单位，小数点后应为2位，末位为估读位.故三个数据中不符合有效数字读数要求的是OC段，应记作15.70 cm.

(2)OB段重力势能的减少量为：

E_p＝mgh＝m×9.8×12.42×10^－2≈1.22m

与B点对应的重物运动的瞬时速度为：

v_B＝ m/s≈1.5475 m/s

与B点对应的重物的动能E_kB＝m×1.5475²≈1.20m

即动能的增加量ΔE_k＝1.20m

这样验证的系统误差是使重力势能的减少量大于动能的增加量，原因是速度v是实际速度，因为有摩擦，减少的重力势能一部分转化为内能.

(3)v_B＝gt＝9.8×8×0.02 m/s＝1.568 m/s

所以E_kB＝m×1.568²≈1.23m

这样验证的系统误差总是使重力势能的减少量小于动能的增加量，是因为速度v是按照自由落体运动计算的，对应的下落高度比实际测得的高度要大.

答案：(1)OC　15.70　(2)1.22m　1.20m　大于　速度v是实际速度，因为有摩擦，减少的重力势能一部分转化为内能

(3)1.23m　小于　速度v是按照自由落体运动计算的，对应的下落高度比实际测得的高度要大

5.(11分)在利用重物自由下落验证机械能守恒定律的实验中

(1)某同学在实验中得到的纸带如图所示，其中A、B、C、D是打下的相邻的四个点，它们到运动起始点O的距离分别为62.99 cm、70.18 cm、77.76 cm、85.73 cm.已知当地的重力加速度g＝9.80 m/s²，打点计时器所用电源的频率为50 Hz，重物的质量为1.00 kg.请根据以上数据计算重物由O点运动到C点的过程中，重力势能的减少量为　　J，动能的增加量为　　J.(结果均保留三位有效数字)

(2)甲、乙、丙三名同学通过实验各得到一条纸带，它们前两个点间的距离分别是1.0 mm、1.9 mm、4.0 mm.那么操作中一定存在错误的同学是　　，造成错误的原因是　　　　　　　　　　　　　　.

解析：(1)ΔE_p＝mg·OC＝7.62 J

v_C＝＝3.89 m/s，E_kC＝mv＝7.57 J.

(2)丙得到的距离4.00 mm明显大于2.00 mm，故其错误，说明打第一个点时纸带有初速度.

答案：(1)7.62　7.57

(2)丙　先释放重物，后接通电源