上海市2009年高考模拟试题汇编
数列
一、填空题
1、(2009上海九校联考)已知数列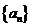 的前
的前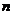 项和为
项和为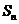 ,若
,若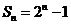 ,则
,则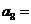 .
.
128
2、((2009上海八校联考)在数列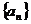 中,
中,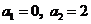 ,且
,且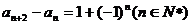 ,
,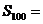 _________。
_________。
2550
3、(2009冠龙高级中学3月月考)若数列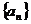 中,
中,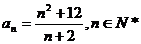 ,则数列
,则数列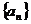 中的项的最小值为_________。
中的项的最小值为_________。
4
4、(2009闵行三中模拟)已知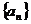 是等比数列,
是等比数列,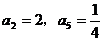 ,则
,则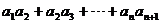 = 。
= 。
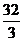 (
(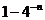 )
)
5、(2009上海十四校联考)若数列 为“等方比数列”。则“数列
为“等方比数列”。则“数列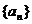 是等方比数列”是“数列
是等方比数列”是“数列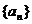 是等方比数列”的 条件
是等方比数列”的 条件
2
二、选择题
1、(2009上海十四校联考)无穷等比数列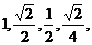 …各项的和等于 ( )
…各项的和等于 ( )
A.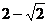 B.
B.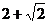 C.
C.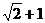 D.
D.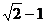
B
2、(2009上海卢湾区4月模考)
设数列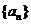 的前
的前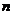 项之和为
项之和为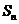 ,若
,若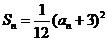 (
(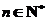 ),则
),则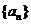 ( )
( )
A.是等差数列,但不是等比数列; B.是等比数列,但不是等差数列;
C.是等差数列,或是等比数列; D.可以既不是等比数列,也不是等差数列.
三、解答题
1、(2009上海卢湾区4月模考)已知数列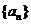 的前
的前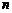 项和为
项和为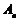 ,且对任意正整数
,且对任意正整数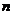 ,都满足:
,都满足: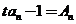 ,其中
,其中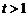 为实数.
为实数.
(1)求数列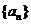 的通项公式;
的通项公式;
(2)若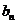 为杨辉三角第
为杨辉三角第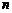 行中所有数的和,即
行中所有数的和,即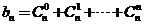 ,
,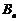 为杨辉三角前
为杨辉三角前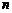 行中所有数的和,亦即为数列
行中所有数的和,亦即为数列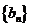 的前
的前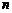 项和,求
项和,求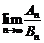 的值.
的值.
解:(1) 由已知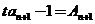 ,
,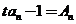 ,相减得
,相减得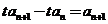 ,由
,由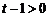 得
得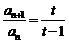 ,又
,又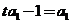 ,得
,得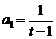 ,故数列
,故数列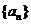 是一个以
是一个以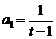 为首项,以
为首项,以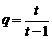 为公比的等比数列.
(4分)
为公比的等比数列.
(4分)
从而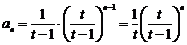
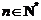 ;
(6分)
;
(6分)
(2)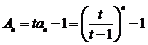 ,
(7分)
,
(7分)
又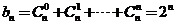 ,故
,故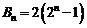 ,
(11分)
,
(11分)
于是 ,
,
当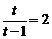 ,即
,即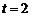 时,
时,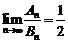 ,
,
当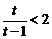 ,即
,即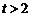 时,
时,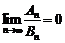 ,
,
当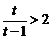 ,即
,即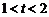 时,
时,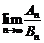 不存在.
(14分)
不存在.
(14分)
2、(2009上海八校联考)已知点列
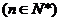 顺次为直线
顺次为直线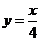 上的点,点列
上的点,点列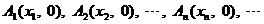
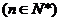 顺次为
顺次为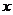 轴上的点,其中
轴上的点,其中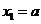
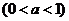 ,对任意的
,对任意的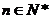 ,点
,点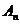 、
、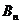 、
、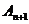 构成以
构成以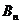 为顶点的等腰三角形。
为顶点的等腰三角形。
(1)证明:数列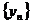 是等差数列;
是等差数列;
(2)求证:对任意的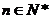 ,
,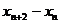 是常数,并求数列
是常数,并求数列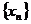 的通项公式;
的通项公式;
(3)对上述等腰三角形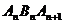 添加适当条件,提出一个问题,并做出解答。
添加适当条件,提出一个问题,并做出解答。
(根据所提问题及解答的完整程度,分档次给分)
解: (1)依题意有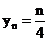 ,于是
,于是 .
.
所以数列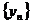 是等差数列.
是等差数列.
 .4分
.4分
(2)由题意得 ,即
,即 , (
, (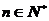 )
①
)
①
所以又有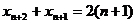 .
②
.
②
由②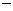 ①得:
①得: , 所以
, 所以 是常数.
是常数.  6分
6分
由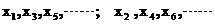 都是等差数列.
都是等差数列.
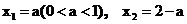 ,那么得
,那么得  ,
,
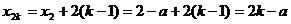 . (
. (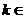

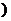
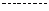 8分
8分
故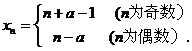
 10分
10分
(3) 提出问题①:若等腰三角形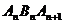 中,是否有直角三角形,若有,求出实数
中,是否有直角三角形,若有,求出实数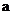
提出问题②:若等腰三角形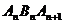 中,是否有正三角形,若有,求出实数
中,是否有正三角形,若有,求出实数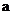
解:问题① 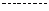 11分
11分
当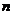 为奇数时,
为奇数时,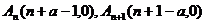 ,所以
,所以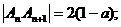
当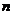 为偶数时,
为偶数时,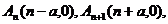 所以
所以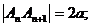
作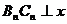 轴,垂足为
轴,垂足为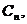 则
则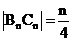 ,要使等腰三角形
,要使等腰三角形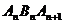 为直角三角形,必须且只须:
为直角三角形,必须且只须: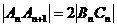 .
.
 13分
13分
当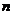 为奇数时,有
为奇数时,有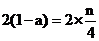 ,即
,即 ①
①
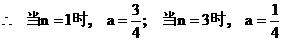 , 当
, 当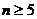 ,
, 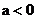 不合题意.
不合题意.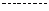 15分
15分
当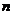 为偶数时,有
为偶数时,有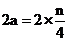 ,
,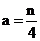 ,同理可求得
,同理可求得 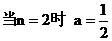
当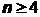 时,
时,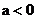 不合题意.
不合题意.  17分
17分
综上所述,使等腰三角形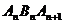 中,有直角三角形,
中,有直角三角形,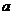 的值为
的值为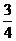 或
或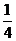 或
或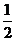 .
.
 18分
18分
解:问题②  11分
11分
当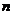 为奇数时,
为奇数时,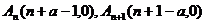 ,所以
,所以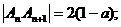
当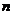 为偶数时,
为偶数时,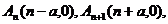 所以
所以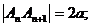
作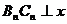 轴,垂足为
轴,垂足为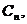 则
则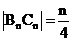 ,要使等腰三角形
,要使等腰三角形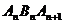 为正三角形,必须且只须:
为正三角形,必须且只须: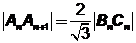 .
.
 13分
13分
当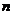 为奇数时,有
为奇数时,有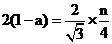 ,即
,即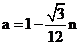 ①
①
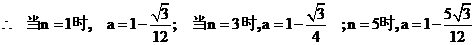 , 当
, 当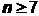 时,.
时,. 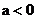 不合题意.
不合题意.  15分
15分
当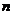 为偶数时,有
为偶数时,有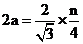 ,
,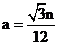 ,同理可求得
,同理可求得 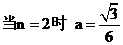 .
.
 ;
;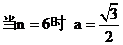 ;当
;当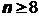 时,
时,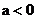 不合题意.
不合题意. 17分
17分
综上所述,使等腰三角形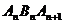 中,有正三角形,
中,有正三角形,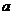 的值为
的值为
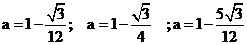 ;
;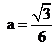 ;
;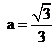 ;
;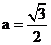
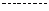 18分
18分
3、(2009上海奉贤区模拟考)已知点集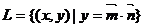 ,其中
,其中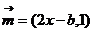 ,
,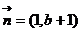 ,点列
,点列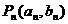 在L中,
在L中, 为L与y轴的交点,等差数列
为L与y轴的交点,等差数列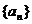 的公差为1,
的公差为1,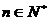 。
。
(1)求数列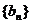 的通项公式;
的通项公式;
(2)若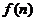 =
= ,令
,令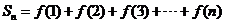 ;试用解析式写出
;试用解析式写出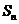 关于
关于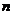 的函数。
的函数。
(3)若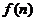 =
= ,给定常数m(
,给定常数m( ),是否存在
),是否存在 ,使得
,使得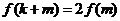 ,若存在,求出
,若存在,求出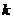 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(1)y= ?
? =(2x-b)+(b+1)=2x+1
-----(1分)
=(2x-b)+(b+1)=2x+1
-----(1分)
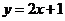 与
与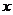 轴的交点
轴的交点 为
为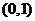 ,所以
,所以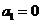 ;
-----(1分)
;
-----(1分)
所以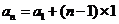 ,即
,即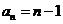 ,
-----(1分)
,
-----(1分)
因为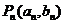 在
在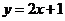 上,所以
上,所以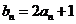 ,即
,即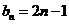 -----(1分)
-----(1分)
(2)设
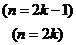 (
(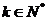 ),
),
即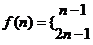
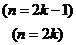 (
(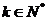 ) ----(1分)
) ----(1分)
(A)当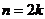 时,
时,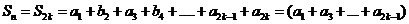
 ----(1分)
----(1分)
=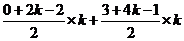 =
=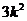 ,而
,而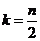 ,所以
,所以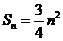 ----(1分)
----(1分)
(B)当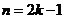 时,
时,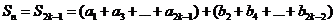 ----(1分)
----(1分)
= 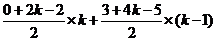 =
=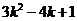 ,
----(1分)
,
----(1分)
而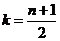 ,所以
,所以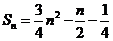 ----(1分)
----(1分)
因此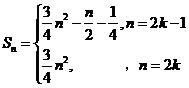 (
(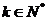 ) ----(1分)
) ----(1分)
(3)假设 ,使得
,使得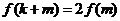 ,
,
(A)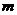 为奇数
为奇数
(一)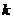 为奇数,则
为奇数,则 为偶数。则
为偶数。则 ,
,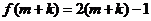 。则
。则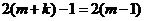 ,解得:
,解得: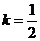 与
与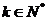 矛盾。
----(1分)
矛盾。
----(1分)
(二)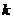 为偶数,则
为偶数,则 为奇数。则
为奇数。则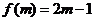 ,
,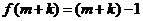 。则
。则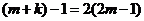 ,解得:
,解得: (
( 是正偶数)。 ----(1分)
是正偶数)。 ----(1分)
(B)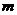 为偶数
为偶数
(一)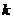 为奇数,则
为奇数,则 为奇数。则
为奇数。则 ,
,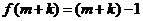 。则
。则 ,解得:
,解得: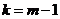 (
(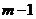 是正奇数)。
----(1分)
是正奇数)。
----(1分)
(二)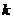 为偶数,则
为偶数,则 为偶数。则
为偶数。则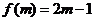 ,
,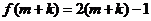 。则
。则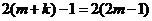 ,解得:
,解得: 与
与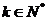 矛盾。 ----(1分)
矛盾。 ----(1分)
由此得:对于给定常数m( ),这样的
),这样的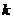 总存在;当
总存在;当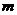 是奇数时,
是奇数时, ;当
;当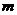 是偶数时,
是偶数时,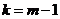 。
----(1分)
。
----(1分)
4、(2009冠龙高级中学3月月考)由函数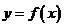 确定数列
确定数列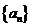 ,
,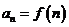 ,函数
,函数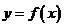 的反函数
的反函数 能确定数列
能确定数列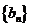 ,
,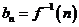 ,若对于任意
,若对于任意 ,都有
,都有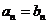 ,则称数列
,则称数列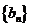 是数列
是数列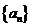 的“自反数列”。
的“自反数列”。
(1)若函数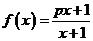 确定数列
确定数列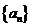 的自反数列为
的自反数列为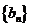 ,求
,求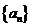 的通项公式;
的通项公式;
(2)在(1)条件下,记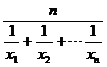 为正数数列
为正数数列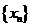 的调和平均数,若
的调和平均数,若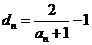 ,
,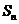 为数列
为数列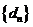 的前
的前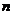 项和,
项和,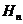 为数列
为数列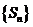 的调和平均数,求
的调和平均数,求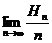 ;
;
(3)已知正数数列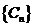 的前
的前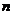 项之和
项之和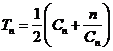 。求
。求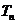 的表达式。
的表达式。
解:(1)由题意的:f ?1(x)=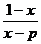 = f(x)=
= f(x)=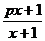 ,所以p = ?1,所以an=
,所以p = ?1,所以an=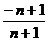
(2) an=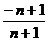 ,dn=
,dn=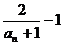 =n,
=n,
Sn为数列{dn}的前n项和,Sn=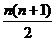 ,又Hn为数列{Sn}的调和平均数,
,又Hn为数列{Sn}的调和平均数,
Hn=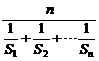 =
=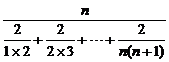 =
=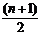
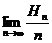 =
=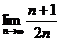 =
=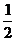
(3)因为正数数列{cn}的前n项之和Tn=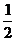 (cn+
(cn+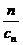 ),
),
所以c1=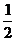 (c1+
(c1+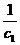 ),解之得:c1=1,T1=1
),解之得:c1=1,T1=1
当n≥2时,cn = Tn?Tn?1,所以2Tn = Tn?Tn?1 +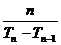 ,
,
Tn +Tn?1 = 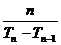 ,即:
,即: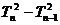 = n,
= n,
所以,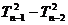 = n?1,
= n?1,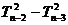 = n?2,……,
= n?2,……,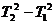 =2,累加得:
=2,累加得:
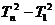 =2+3+4+……+ n,
=2+3+4+……+ n, 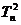 =1+2+3+4+……+
n =
=1+2+3+4+……+
n =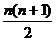 ,Tn=
,Tn=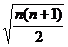
5、(2009闵行三中模拟)已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn)(n∈N)顺次为一次函数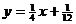 图像上的点,点列A1(x1,0)、A2(x2,0)、…、An(xn,0)(n∈N)顺次为x轴正半轴上的点,其中x1=a(0<a<1),对于任意n∈N,点An、Bn、An+1构成一个顶角的顶点为Bn的等腰三角形。
图像上的点,点列A1(x1,0)、A2(x2,0)、…、An(xn,0)(n∈N)顺次为x轴正半轴上的点,其中x1=a(0<a<1),对于任意n∈N,点An、Bn、An+1构成一个顶角的顶点为Bn的等腰三角形。
⑴求数列{yn}的通项公式,并证明{yn}是等差数列;
⑵证明xn+2-xn为常数,并求出数列{xn}的通项公式;
 ⑶在上述等腰三角形AnBnAn+1中,是否存在直角三角形?若有,求出此时a值;若不存在,请说明理由。
⑶在上述等腰三角形AnBnAn+1中,是否存在直角三角形?若有,求出此时a值;若不存在,请说明理由。
解:(1) (nÎN),∵yn+1-yn=
(nÎN),∵yn+1-yn=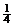 ,∴{yn}为等差数列 ………………4分
,∴{yn}为等差数列 ………………4分
(2)因为 与
与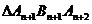 为等腰三角形.
为等腰三角形.
所以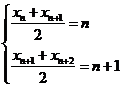 ,两式相减得
,两式相减得  。………………7分
。………………7分
注:判断 得2分,证明得1分
得2分,证明得1分
∴x1,x3,x5,…,x2n-1及x2,x4,x6 ,…,x2n都是公差为2的等差数列,………………6分
∴ ………………10分
………………10分
(3)要使AnBnAn+1为直角三形,则 |AnAn+1|=2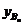 =2(
=2(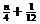 )Þxn+1-xn=2(
)Þxn+1-xn=2(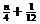 )
)
当n为奇数时,xn+1=n+1-a,xn=n+a-1,∴xn+1-xn=2(1-a).
Þ2(1-a)=2(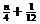 ) Þa=
) Þa=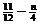 (n为奇数,0<a<1) (*)
(n为奇数,0<a<1) (*)
取n=1,得a=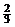 ,取n=3,得a=
,取n=3,得a=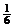 ,若n≥5,则(*)无解; ………………14分
,若n≥5,则(*)无解; ………………14分
当偶数时,xn+1=n+a,xn=n-a,∴xn+1-xn=
∴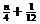 )Þa=
)Þa=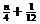 (n为偶数,0<a<1) (*¢),
(n为偶数,0<a<1) (*¢),
取n=2,得a= ,若n≥4,则(*¢)无解.
,若n≥4,则(*¢)无解.
综上可知,存在直角三形,此时a的值为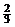 、
、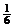 、
、 . ………………18分
. ………………18分
 |
6、(2009上海青浦区)设数列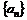 的前
的前 和为
和为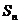 ,已知
,已知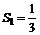 ,
,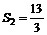 ,
,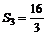 ,
,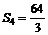 ,
,
一般地,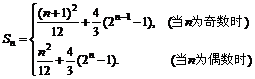 (
(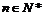 ).
).
(1)求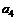 ;
;
(2)求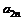 ;
;
(3)求和: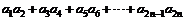 .
.
(1)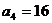 ;
……3分
;
……3分
(2)当 时,(
时,(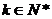 )
)
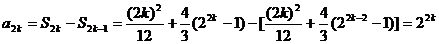 , ……6分
, ……6分
所以,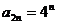 (
(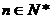 ).
……8分
).
……8分
(3)与(2)同理可求得: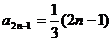 ,
……10分
,
……10分
设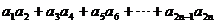 =
=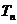 ,
,
则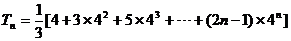 ,(用等比数列前n项和公式的推导方法)
,(用等比数列前n项和公式的推导方法) ,相减得
,相减得
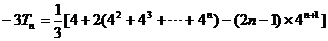 ,所以
,所以
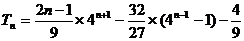 .
……14分
.
……14分