摘要:(1)求数列的通项公式,
网址:http://m.1010jiajiao.com/timu_id_119003[举报]



⑴求数列
 的通项公式;
的通项公式;⑵设
 ,若
,若 对
对 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;⑶是否存在以
 为首项,公比为
为首项,公比为 的数列
的数列 ,
, ,使得数列
,使得数列 中每一项都是数列
中每一项都是数列 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列 的通项公式;若不存在,说明理由
的通项公式;若不存在,说明理由设数列![]() 的通项公式为
的通项公式为![]() 。数列
。数列![]() 定义如下:对于正整数m,
定义如下:对于正整数m,![]() 是使得不等式
是使得不等式![]() 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若![]() ,求b3; (2)若
,求b3; (2)若![]() ,求数列
,求数列![]() 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得![]() ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。
 的通项公式为
的通项公式为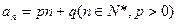 。数列
。数列 定义如下:对于正整数m,
定义如下:对于正整数m, 是使得不等式
是使得不等式 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若 ,求b3; (2)若
,求b3; (2)若 ,求数列
,求数列 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得 ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。