摘要:(1)若函数确定数列的自反数列为.求的通项公式,
网址:http://m.1010jiajiao.com/timu_id_119073[举报]
由函数![]() 确定数列
确定数列![]() ,
,![]() ,函数
,函数![]() 的反函数
的反函数![]() 能确定数列
能确定数列![]() ,
,![]() ,若对于任意
,若对于任意![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 是数列
是数列![]() 的“自反数列”。
的“自反数列”。
(1)若函数![]() 确定数列
确定数列![]() 的自反数列为
的自反数列为![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)在(1)条件下,记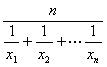 为正数数列
为正数数列![]() 的调和平均数,若
的调和平均数,若![]() ,
,
![]() 为数列
为数列![]() 的前
的前![]() 项和,
项和,![]() 为数列
为数列![]() 的调和平均数,求
的调和平均数,求![]() ;
;
(3)已知正数数列![]() 的前
的前![]() 项之和
项之和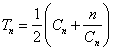 。求
。求![]() 的表达式。
的表达式。
查看习题详情和答案>>
由函数y=f(x)确定数列{an},an=f(n),函数y=f(x)的反函数y=f-1(x)能确定数列bn,bn=f-1(n)若对于任意n∈N*都有bn=an,则称数列{bn}是数列{an}的“自反函数列”
(1)设函数f(x)=
,若由函数f(x)确定的数列{an}的自反数列为{bn},求an;
(2)已知正整数列{cn}的前项和sn=
(cn+
).写出Sn表达式,并证明你的结论;
(3)在(1)和(2)的条件下,d1=2,当n≥2时,设dn=
,Dn是数列{dn}的前n项和,且Dn>loga(1-2a)恒成立,求a的取值范围.
查看习题详情和答案>>
(1)设函数f(x)=
| px+1 |
| x+1 |
(2)已知正整数列{cn}的前项和sn=
| 1 |
| 2 |
| n |
| cn |
(3)在(1)和(2)的条件下,d1=2,当n≥2时,设dn=
| -1 |
| anSn2 |
由函数y=f(x)确定数列{an},an=f(n),函数y=f(x)的反函数y="f" -1(x)能确定数列{bn},bn=" f" –1(n),若对于任意nÎN*,都有bn=an,则称数列{bn}是数列{an}的“自反数列”.
(1)若函数f(x)= 确定数列{an}的自反数列为{bn},求an;
确定数列{an}的自反数列为{bn},求an;
(2)已知正数数列{cn}的前n项之和Sn= (cn+
(cn+ ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论;
(3)在(1)和(2)的条件下,d1=2,当n≥2时,设dn= ,Dn是数列{dn}的前n项之和,且Dn>log a (1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项之和,且Dn>log a (1-2a)恒成立,求a的取值范围.
 确定数列{an}的自反数列为{bn},求an;
确定数列{an}的自反数列为{bn},求an; (cn+
(cn+ ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论; ,Dn是数列{dn}的前n项之和,且Dn>log a (1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项之和,且Dn>log a (1-2a)恒成立,求a的取值范围.