摘要:(2)若为杨辉三角第行中所有数的和.即.为杨辉三角前行中所有数的和.亦即为数列的前项和.求的值.
网址:http://m.1010jiajiao.com/timu_id_119004[举报]
杨辉是中国南宋末年的一位杰出的数学家、数学教育家、杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律.如图所示是一个11阶杨辉三角:

(1)求第20行中从左到右的第4个数;
(2)若第n行中从左到右第14与第15个数的比为
,求n的值;
(3)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数.试用含有m,k(m,k∈N*)的数学公式表示上述结论,并给予证明.
查看习题详情和答案>>

(1)求第20行中从左到右的第4个数;
(2)若第n行中从左到右第14与第15个数的比为
| 2 | 3 |
(3)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数.试用含有m,k(m,k∈N*)的数学公式表示上述结论,并给予证明.
已知数列{an}的前n项和为An,且对任意正整数n,都满足:tan-1=An,其中t>1为实数.
(1)求数列{an}的通项公式;
(2)若bn为杨辉三角第n行中所有数的和,即bn=Cn+Cn1+…+Cnn,Bn为杨辉三角前n行中所有数的和,亦即为数列{bn}的前n项和,求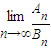 的值.
的值.
查看习题详情和答案>>
(1)求数列{an}的通项公式;
(2)若bn为杨辉三角第n行中所有数的和,即bn=Cn+Cn1+…+Cnn,Bn为杨辉三角前n行中所有数的和,亦即为数列{bn}的前n项和,求
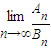 的值.
的值.查看习题详情和答案>>
已知数列{an}的前n项和为An,且对任意正整数n,都满足:tan-1=An,其中t>1为实数.
(1)求数列{an}的通项公式;
(2)若bn为杨辉三角第n行中所有数的和,即bn=Cn+Cn1+…+Cnn,Bn为杨辉三角前n行中所有数的和,亦即为数列{bn}的前n项和,求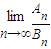 的值.
的值.
查看习题详情和答案>>
(1)求数列{an}的通项公式;
(2)若bn为杨辉三角第n行中所有数的和,即bn=Cn+Cn1+…+Cnn,Bn为杨辉三角前n行中所有数的和,亦即为数列{bn}的前n项和,求
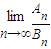 的值.
的值.查看习题详情和答案>>
(2009•卢湾区二模)已知数列{an}的前n项和为An,且对任意正整数n,都满足:tan-1=An,其中t>1为实数.
(1)求数列{an}的通项公式;
(2)若bn为杨辉三角第n行中所有数的和,即bn=Cn0+Cn1+…+Cnn,Bn为杨辉三角前n行中所有数的和,亦即为数列{bn}的前n项和,求
的值.
查看习题详情和答案>>
(1)求数列{an}的通项公式;
(2)若bn为杨辉三角第n行中所有数的和,即bn=Cn0+Cn1+…+Cnn,Bn为杨辉三角前n行中所有数的和,亦即为数列{bn}的前n项和,求
| lim |
| n→∞ |
| An |
| Bn |
杨辉是中国南宋末年的一位杰出的数学家、数学教育家、杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律.下图是一个11阶杨辉三角:

(1)求第20行中从左到右的第4个数;
(2)若第n行中从左到右第14与第15个数的比为![]() ,求n的值;
,求n的值;
(3)若n阶(包括0阶)杨辉三角的所有数的和;
(4)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:
第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数.
试用含有m、k(m,k∈N*)的数学公式表示上述结论,并给予证明.