江苏省南京市2007届高三质量检测数学试卷
本试卷分第Ⅰ卷(选择题)和第lI卷(非选择题)两部分,共150分.考试用时120分钟.
注意事项:
答题前考生务必将学校、姓名、班级、学号写在答卷纸的密封线内.每题答案写在答卷纸上对应题目的答案空格里,答案不写在试卷上.考试结束,将答卷纸交回.
参考公式:
如果事件A、B互斥,那么 正棱锥、圆锥的侧面积公式
P(A+B)=P (A)+P(B) S =
= cl
cl
如果事件A、B相独立,那么 其中c表示底面周长,l表
P(A?B)=P(A)?P(B) 示斜高或母线长
如果事件A在一次试验中发生的概率是P,那 球的表面积公式
么n次独立重复试验中恰好发生k次的概率 S
P (k)=C
(k)=C P
P (1-P)
(1-P) 其中R表示球的半径
其中R表示球的半径
第Ⅰ卷(选择题 共50分)
一、择题题:本大题共10小题;每小题5分,共50分.在每小题给出的四个选顶中,有且只有一项是符合题目要求的.
1.已知全集U={1,2,3,
4,5,6},集合P={1,2,3,4},Q={3,4,5,6},则P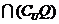
A.{1,2} B.{3,4} C.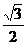 D.1
D.1
2.已知a=(cos40°,sin40°),b+(sin20°,cos20°),则a?b的值为
A.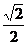 B.
B.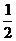 C.
C.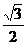 D.1
D.1
3.将函数y=sin2x的图象按向量a=(-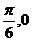 )平移后的图象的函数解析式为
)平移后的图象的函数解析式为
A.y=sin(2x+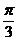 ) B. y=sin(2x-
) B. y=sin(2x-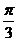 ) C. y=sin(2x+
) C. y=sin(2x+ ) D. y=sin(2x-
) D. y=sin(2x- )
)
4.已知双曲线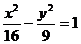 ,双曲线上的点P到左焦点的距离与点P到左准线的距离之比等于
,双曲线上的点P到左焦点的距离与点P到左准线的距离之比等于
A.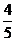 B.
B.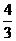 C.
C.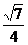 D.
D.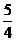
5.(2x+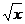 )
)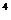 的展开式中的x
的展开式中的x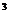 系数是
系数是
A.6 B.
6.下列函数中,在其定义域内既是奇函数又是减函数的是
A.y=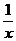 B.y=2
B.y=2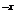 C.y=lg
C.y=lg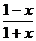 D.
D.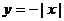
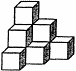 7.将棱长相等的正方体按右图所示的形状摆放,从上往下依次为第一层,第二层,第三层…,则第6层正方体的个数是
7.将棱长相等的正方体按右图所示的形状摆放,从上往下依次为第一层,第二层,第三层…,则第6层正方体的个数是
A.28 B.21 C.15 D.11
8.设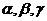 为两两不重合的平面,
为两两不重合的平面,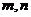 为两条不重合的直线,给出下列四个命题:
为两条不重合的直线,给出下列四个命题:
①若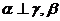 ∥
∥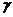 ,则
,则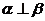 ;
;
②若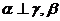 ∥
∥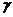 ,则
,则 ∥
∥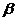 ;
;
③若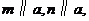

④若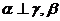 ⊥
⊥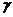 ,
,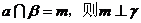 .
.
其中真命题的个数是
A.1 B.2 C.3 D.4
9.若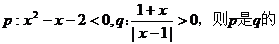
A.充分不必要条件 B.必要不充分
C.充要条件 D.既不充分也不必要条件
10.如果一条直线与一个平面平行,那么,称此直线与平构成一个“平行线面线”.在一个平行六面体中,由两个顶点确定的直线与含有四个顶点的平面构成的“平行线面线”的个数是
A.60 B.48 C.36 D.24
第Ⅱ卷(非选择题 共100分)
二、填空题:本大题共6小题;每小题5分,共30分.把答案填在题中的横线上.
11.一个电视台在因特网上就观众对其某一节止的喜爱程度进行调查,参加调查的总人数为15000人,其中持各种态度的人数如下表所示:
很喜爱
喜爱
一般
不喜爱
3000
4500
5000
2500
电视台为了了解观众的具体想法和意见,打算从中抽取选出150人进行更为详细的调查,为此要进行分层抽样,那么在“喜爱”这类态度的观众中抽取的人数为_____________
12.已知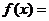 log
log ,函数g(x)的图象与函数f(x)的图象关于直线y=x对称,则g(1)=____________
,函数g(x)的图象与函数f(x)的图象关于直线y=x对称,则g(1)=____________
13.已知圆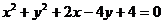 关于直线y=2x+b成轴对称,则b=_________.
关于直线y=2x+b成轴对称,则b=_________.
14.函数 的最小正周期是______________.
的最小正周期是______________.
15.一个正四棱柱的顶点都在球面上,底面边长为1,高为2,则此球的表面积为________.
16.已知抛物线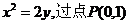 的直线与抛物线相交于
的直线与抛物线相交于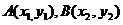 两点,则
两点,则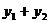 的最小值是___________.
的最小值是___________.
三、解答题:本大题5小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分,第一小问满分6分,第二小问满分6分)
已知数列(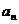 )是等差数列,(
)是等差数列,(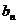 )是等比数列,且a1=b1=2,b4=54,a1+a3=b2+b3.
)是等比数列,且a1=b1=2,b4=54,a1+a3=b2+b3.
(1)求数列{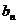 }的通项公式
}的通项公式
(2)求数列{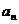 }的前10项和S
}的前10项和S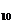 .
.
18.(本小题满分14分,第一小问满分6分,第二小问满分8分)
一个口袋内装有大小相同且已编有不同号码的4个黑球和3个红球,某人一次从中摸出2个球。
(1)如果摸到球中含有红球就中奖, 那么此人中奖的概率是多少?
(2)如果摸到的两个球都时红球,那么就中大奖,在有放回的3次摸球中,此人恰好两次中大奖的概率是多少?
19.(本小题满分16分,第一小问满分5分,第二小问满分5分,第三小问满分6分)
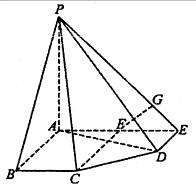
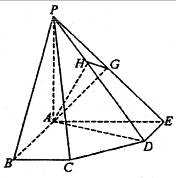
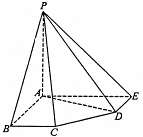 在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=
在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=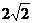 a,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.
a,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.
(1)求证:PA⊥平面ABCDE;
(2)求二面角A-PD-E的大小;
(3)求点C到平面PDE的距离.
20.(本小题满分14分,第一小问满分4分,第二小问满分5分,第三小问满分5分)
在直角坐标系中,O为坐标原点,设直线l经过点P(3,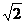 ),且与x轴交于点F(2,0).
),且与x轴交于点F(2,0).
(1)求直线l的方程;
(2)如果一个椭圆经过点P,且以点F为它的一个焦点,求椭圆的标准方程;
(3)若在(Ⅰ)(Ⅱ)的情况下,设直线l与椭圆的另一个交点Q,且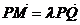 ,当|
,当|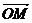 |最小时,求
|最小时,求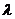 对应值.
对应值.
21.(本小题满分14分,第一小问满分4分,第二小问满分5分,第三小问满分5分)
已知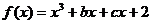 .
.
(1)若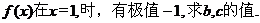
(2)当b为非零实数时,证明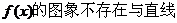 (
( -c)
-c)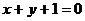 平行的切线;
平行的切线;
(3)记函数|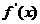 |(-1≤x≤1)的最大值为M,求证:M≥
|(-1≤x≤1)的最大值为M,求证:M≥ .
.
南京市2007届高三质量检测数学答案及评分标准
说明:
题号
1
2
3
4
5
6
7
8
9
10
答案
A
C
A
D
C
C
B
C
D
B
二、填空题:每小题5分,满分30分.
11.45 12.0 13.4 14.π 15.6π 16.2
三、解答题
17.(1)∵{bn}是等比数列,且b1=2,b4=54,
∴q3=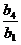 =27. 3分
=27. 3分
∴q=3. ∴bn=b1?qn-1=2?3n-1. 6分
(2)∵数列{an}是等差数列,a1+a2+a3=b2+b3,
又b2+b3=6+18=24,∴a1+a2+a3=3a2=24,∴a2=8.
从而d=a2-a1=8-2=6. 9分
∴a10=a1+(10-1)d=2+9×6=56.
∴S10=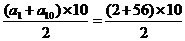 =290
12分
=290
12分
18.(1)记“从袋中摸出的两个球中含有红球”为事件A, 1分
则P(B)=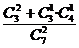 =
=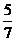 . 5分
. 5分
(或“不含红球即摸出的两个球都是黑球”为事件)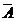 .
.
∵P(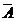 )=
)=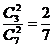 .∴P(A)=-1-P(
.∴P(A)=-1-P(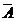 )=
)=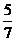 . 5分
. 5分
答:此人中奖的概率是 . 6分
. 6分
(2)记从“袋中摸出的两个球都是红球”为事件B, 7分
则P(B)= =
=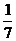 . 10分
. 10分
由于有放回的3次摸,每次是否摸到两个红球之间没有影响.
所以3次摸球恰好有两次中大奖相当于作3次独立重复试验,
根据n次独立重复试验中事件恰好发生k次的概率公式得,
P3(2)=C23(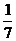 )2?(1-
)2?(1-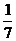 )3-2=
)3-2=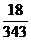 . 13分
. 13分
答:此人恰好两倍欠中大奖的概率是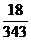 . 14分
. 14分
19.(1)证明∵PA=AB=2a,PB=2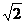 a,
a,
∴PA2+AB2=PB2,∴∠PAB=90°,即PA⊥AB.
同理PA⊥AE. 3分
∵AB∩AE=A,∴PA⊥平面ABCDE. 5分
 (2)解法一:∵∠AED=90°,
(2)解法一:∵∠AED=90°,
∴AE⊥ED.
∵PA⊥平面ABCDE,
∴PA⊥ED.
∴ED⊥平面PAE.
过A作AG⊥PE于G,
过DE⊥AG,
∴AG⊥平面PDE.
过G作GH⊥PD于H,连AH,
由三垂线定理得AH⊥PD.
∴∠AHG为二面角A-PD-E的平面角. 8分
在直角△PAE中,AG=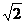 a.
a.
在直角△PAD中,AH=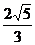 a,
a,
∴在直角△AHG中,sin∠AHG=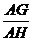 =
=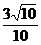 .∴∠AHG=arcsin
.∴∠AHG=arcsin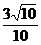 .
.
∴二面角A-PD-E的大小为arcsin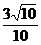 . 10分
. 10分
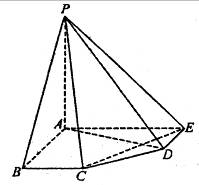 解法二:建立如图所示的直角坐标系,
解法二:建立如图所示的直角坐标系,
则B(2a,0,0),E(0,2a,0),P(0,0,2a),D(a,2a,0),C(2a,a,0),
过A作AN⊥PD于N,
∵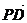 =(a,2a,-2a),
=(a,2a,-2a),
设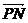 =λ
=λ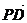 ,
,
∴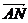 =
=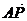 +
+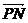 =(λa,2λa,2a-2λa)
=(λa,2λa,2a-2λa)
∵AN⊥PD,
∴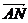 ?
?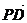 =0.
=0.
∴a?λa+2a?2λa-2a?(2a-2λa)=0.
解得λ=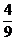 .
.
∴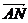 =(
=(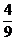 a,
a,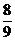 a,
a,  a)
a)
即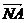 =(-
=(-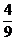 a, -
a, -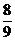 a, -
a, - a)
a)
同理,过E作EM⊥PD于M,
则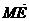 =(-
=(-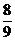 a,
a, 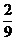 a, -
a, -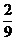 a). 8分
a). 8分
二面角A-PD-E的大小为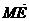 ,
,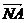 所成的角<
所成的角<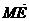 ,
,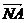 >.
>.
∵cos<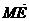 ,
,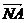 >=arccos=
>=arccos=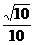 .
.
∴<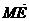 ,
,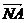 >=arccos=
>=arccos=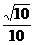 .
.
∴二面角A-PD-E的大小为arccos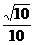 . 10分
. 10分
 (3)解法一:∵∠EAB=∠ABC=∠DEA=90°,
(3)解法一:∵∠EAB=∠ABC=∠DEA=90°,
BC=DE=a,AB=AE=2a,
取AE中点F,连CF,
∵AF∥=BC,
∴四边形ABCF为平行四边形.
∴CF∥AB,而AB∥DE,
∴CF∥DE,而DE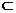 平面PDE,CF
平面PDE,CF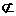 平面PDE,
平面PDE,
∴CF∥平面PDE.
∴点C到平面PDE的距离等于F到平面PDE的距离.
∵PA⊥平面ABCDE,
∴PA⊥DE.
又∵DE⊥AE,∴DE⊥平面PAE.
∴平面PAE⊥平面PDE.∴过F作FG⊥PE于G,则FG⊥平面PDE.
∴FG的长即F点到平面PDE的距离. 13分
在△PAE中,PA=AE=2a,F为AE中点,FG⊥PE,
 ∴FG=
∴FG=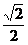 a. ∴点C到平面PDE的距离为
a. ∴点C到平面PDE的距离为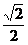 a. 16分
a. 16分
解法二:∵PA平面ABCDE,∴PA⊥DE,
又∵∠DEA=90°,∴DE⊥平面PAE,∴DE⊥PE.
∵BC=DE=a,AB=AE=2a,
连接CE,
则S△CDE=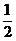 a2,S△DEP=
a2,S△DEP=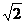 a2 .
a2 .
∵VP-CDE=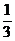 ?PA?S△CDE=
?PA?S△CDE=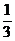 ?2a?
?2a?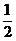 a2=
a2=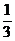 a2. 13分
a2. 13分
设点C到平面PDE的距离为h,
则V C-PDE=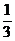 ?h?S△PDE=
?h?S△PDE=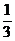 ?h?
?h?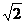 a2=
a2=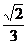 a2h.
a2h.
∵VP-CDE=VC-PDE,
即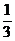 a3=
a3=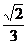 a2h,
a2h,
解得h=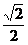 a.即点C到平面PDE的距离为
a.即点C到平面PDE的距离为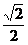 a. 16分
a. 16分
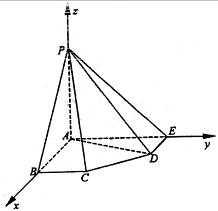 解法三:建立如图所示的直角坐标系,
解法三:建立如图所示的直角坐标系,
则B(2a,0,0),E(0,2a,0),P(0,0,2a),
D(a,2a,0),C(2a,a,0),
设平面PDE的一个法向量为n=(x,y,1),
∵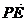 =(0,2a,-2a),
=(0,2a,-2a),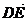 =(-a,0,0),
=(-a,0,0),
又∵n⊥平面PDE.
∴n⊥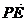 ,n⊥
,n⊥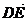 .
.
∴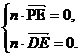
即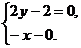
解得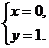
∴n=(0,1,1). 13分
∵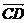 =(-a,a,0),
=(-a,a,0),
∴cos<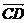 ,n>=
,n>=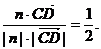
∵0≤<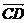 ,n>≤π,
,n>≤π,
∴<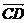 ,n>=
,n>=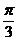 .
.
∵过C作CH⊥平面PDE于H,则CH=|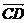 |?|cos<
|?|cos<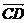 ,n>|,
,n>|,
即点C到平面PDE的距离为
|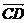 |?|cos<
|?|cos<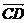 ,n>|=
,n>|=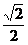 a. 16分
a. 16分
20.(1)∵P(3,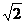 ),F(2,0),
),F(2,0),
∴根据两点式得,所求直线l的方程为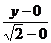 =
=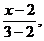
即y=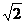 (x-2).
(x-2).
∴直线l的方程是y=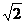 (x-2). 4分
(x-2). 4分
(2)解法一:设所求椭圆的标准方程为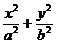 =1(a>b>b),
=1(a>b>b),
∵一个焦点为F(2,0),
∴c=2.
即a2-b2=4 ① 5分
∵点P(3,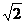 )在椭圆
)在椭圆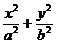 =1(a>b>0)上,
=1(a>b>0)上,
∴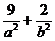 =1 ② 7分
=1 ② 7分
由①,②解得a2=12,b2=8.
所以所求椭圆的标准方程为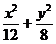 =1. 9分
=1. 9分
解法二:设所求椭圆的标准方程为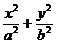 =1(a>b>0),
=1(a>b>0),
∵c=2,a2-b2=4. 6分
∴椭圆的另一个焦点为F1(-2,0).
由椭圆过点P(3,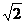 ),
),
∴2a=|PF1|+|PF2|=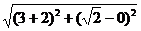 +
+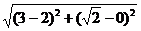 =4
=4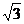 .
.
∴a2=12,b2=8.
所以所求椭圆的标准方程为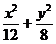 =1. 9分
=1. 9分
(3)解法一:由题意得方程组
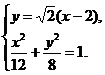 解得
解得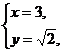 或
或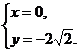
∴Q(0,2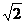 ). 11分
). 11分
 =(-3,-3
=(-3,-3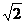 ).
).
∵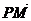 =λ
=λ =(-3λ,3
=(-3λ,3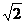 λ),
λ),
∴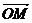 =
=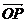 +
+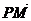 =(3-3λ,
=(3-3λ,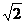 ,3
,3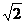 λ).
λ).
∴|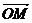 |=
|=
=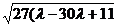 =
=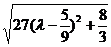 ,
,
∴当λ=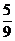 时,|
时,|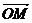 |最小. 14分
|最小. 14分
解法二:由题意得方程组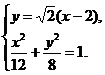 解得
解得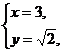 或
或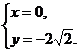
∴Q(0,-2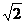 ).
).
∵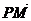 =λ
=λ =(-3λ,3
=(-3λ,3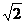 λ),
λ),
∴点M在直线PQ上,∴|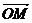 |最小时,必有OM⊥PQ.
|最小时,必有OM⊥PQ.
∴kOM=-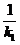 =-
=-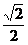 .
.
∴直线OM的方程为y=-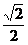 x.
x.
直线OM与PQ的交点为方程组 的解,解之得
的解,解之得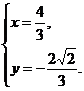
∴M( ,-
,-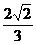 ),∴
),∴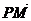 =(-
=(-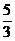 ,-
,-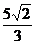 )
)
∵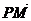 =λ
=λ ,即(-
,即(-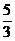 ,-
,-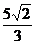 )=λ(-3,-3
)=λ(-3,-3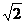 ),∴λ=
),∴λ=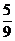 .
.
∴当λ=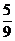 时,|
时,|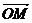 |最小. 14分
|最小. 14分
21.(1)∵f′(x)=3x2+2bx+c,
由f(x)在x=1时,有极值-1得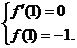 2分
2分
即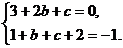 解得
解得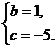 3分
3分
当b=1,c=-5时,f′(x)=3x2+2x-5=(3x+5)(x-1),
当x>1时,f′(x)>0,当-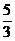 <x<1时,f′(x)<0.
<x<1时,f′(x)<0.
从而符合在x=1时,f(x)有极值.∴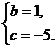 4分
4分
(2)假设f(x)图象在x=t处的切线与直线(b2-c)x+y+1=0平行,
∵f′(t)=3t2+2bt+c,
直线(b2-c)x+y+1=0的斜率为c-b2,
∴3t2+2bt+c=c-b2,
即3t2+2bt+b2=0.
∵△=4(b2-3b2)=-8b2,
又∵b≠0,△<0.
从而方程3t2+2bt+b2=0无解,
因此不存在t,使f′(t)=c-b2,
即f(x)的图象不存在与直线(b2-c)x+y+1=0平行的切线. 9分
(3)证法一:∵|f′(x)|=|3(x+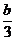 )2+c-
)2+c-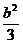 |,
|,
①若|-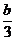 |>1,则M应是|f′(-1)|和|f′(1)|中最大的一个,
|>1,则M应是|f′(-1)|和|f′(1)|中最大的一个,
∴2M≥|f′(-1)|+|f′(1)|=|3-2b+c|+|3+2b+c|≥|4b|>12,
∴M>6,
从而M≥ . 11分
. 11分
②当-3≤b≤0时,2M≥|f′(-1)|+|f′(-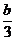 )|=|3-2b+c|+|c-
)|=|3-2b+c|+|c-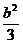 |≥|
|≥|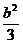 -2b+3|=|
-2b+3|=|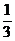 (b-3)2|>3,
(b-3)2|>3,
∴M≥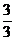 .
.
③当0<b≤3时,2M≥|f′(1)|+|f′(-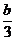 )|=|3+2b+c|+|c-
)|=|3+2b+c|+|c-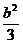 |≥|
|≥|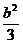 +2b+3|=|
+2b+3|=|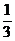 (b+3)2|>3,
(b+3)2|>3,
∴M≥ .
.
综上所述,M≥ . 14分
. 14分
证法二:f′(x)=3x2+2bx+c的顶点坐标是(-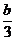 ,
,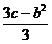 ),
),
①若|-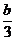 |>1,则M应是|f′(-1)|和|f′(1)|中最大的一个,
|>1,则M应是|f′(-1)|和|f′(1)|中最大的一个,
∴2M≥| f′(-1)|+|f′(1)|=|3-2b+c|+|3+2b+c|≥4|b|>12②
∴M>6,
从而M≥ . 11分
. 11分
②若|-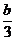 |≤1,则M|f′(-1)|、|f′(1)|、|
|≤1,则M|f′(-1)|、|f′(1)|、|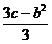 |中最大的一个.
|中最大的一个.
(i)当c≤- 时,2M≥|f′(1)|+
|f′(-1)|≥|f′(1)+ f′(-1)|=|6+2x|≥3,
时,2M≥|f′(1)|+
|f′(-1)|≥|f′(1)+ f′(-1)|=|6+2x|≥3,
M≥ .
.
(ii)当c<- 时,M≥|
时,M≥|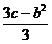 |=
|=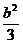 -c≥-c>
-c≥-c> ,
,
综上所述,M≥ 成立. 14分
成立. 14分
证法三:∵M是|f′(x)|,x∈[-1,1]的最大值,
∴M≥|f′(0)|,M≥|f′(1)|,M≥|f′(-1)|. 11分
∴4M≥2|f′(0)|+|f′(1)|+|f′(-1)|≥|f′(1)+f′(-1)-2f′(0)|=6,
即M≥ . 14分
. 14分