摘要：(ii)当c<-时.M≥||=-c≥-c>.
网址：http://m.1010jiajiao.com/timu_id_32778[举报]
已知函数f（x）=4x-k（x2+2clnx）（c＞1，k∈R）有一个极值点是1．
（I）讨论函数f（x）的单调性；
（II）当c＞1时，记f（x）的极大值为M（c），极小值为N（c），对于t∈R，问函数h(c)=M(c)-
N(c)-
是否存在零点？若存在，请确定零点个数；若不存在，请说明理由．
查看习题详情和答案>>
（I）讨论函数f（x）的单调性；
（II）当c＞1时，记f（x）的极大值为M（c），极小值为N（c），对于t∈R，问函数h(c)=M(c)-
| 1 |
| 2 |
| 2c+t |
| c+1 |
（2012•成都一模）设函数f（x）=ax3+bx2+cx，记f（x）的导函数是f′（x）．
（I）当a=-1，b=c=-1时，求函数f（x）的单调区间；
（II）当c=-a2（a＞0）时，若函数f（x）的两个极值点x1、x2满足|x1-x2|=2，求b的取值范围；
（III）若a=-
令h（x）=|f′（x）|，记h（x）在[-1，1]上的最大值为H，当b≥0，c∈R时，证明：H≥
．
查看习题详情和答案>>
（I）当a=-1，b=c=-1时，求函数f（x）的单调区间；
（II）当c=-a2（a＞0）时，若函数f（x）的两个极值点x1、x2满足|x1-x2|=2，求b的取值范围；
（III）若a=-
| 1 |
| 3 |
| 1 |
| 2 |
．
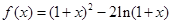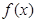的单调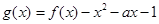区间；
在区间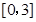
上的最小值．
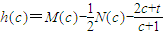是否存在零点？若存在，请确定零点个数；若不存在，请说明理由．