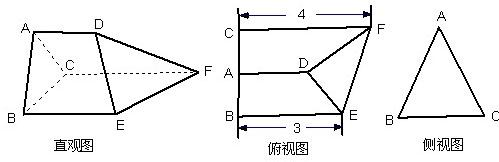
∴CF∥DE.而DE平面PDE.CF平面PDE. ∴CF∥平面PDE． ∴点C到平面PDE的距离等于F到平面PDE的距离． ∵PA⊥平面ABCDE. ∴PA⊥DE．又∵DE⊥AE.∴DE⊥——青夏教育精英家教网——

摘要：∴CF∥DE.而DE平面PDE.CF平面PDE. ∴CF∥平面PDE． ∴点C到平面PDE的距离等于F到平面PDE的距离． ∵PA⊥平面ABCDE. ∴PA⊥DE．又∵DE⊥AE.∴DE⊥平面PAE． ∴平面PAE⊥平面PDE．∴过F作FG⊥PE于G.则FG⊥平面PDE． ∴FG的长即F点到平面PDE的距离． 13分在△PAE中.PA=AE=2a.F为AE中点.FG⊥PE.

网址：http://m.1010jiajiao.com/timu_id_32704[举报]

如图多面体ABCDEF中，ABCD是边长为2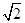的正方形，AE⊥平面ABCD，BF∥AE且AE＝2BF＝4，则以下结论正确的是______________________．（写出所有正确结论的编号）

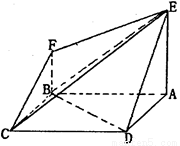
①CF∥DE；②BD∥平面CEF；③AF⊥平面BCE；

④平面CEF⊥平面ADE．

查看习题详情和答案>>

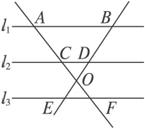
如图1-1-8,直线l1∥l2∥l3,AF、BE交于O,则下列结论中不正确的是( )

图1-1-8

A.AC=BD,CF=DE B. AC=CF,BD=DE

C.AC=BD,CO=OD,OE=OF D.均不正确

查看习题详情和答案>>

（2012•江西）如图，在梯形ABCD中，AB∥CD，E，F是线段AB上的两点，且DE⊥AB，CF⊥AB，AB=12，AD=5，BC=4

，DE=4．现将△ADE，△CFB分别沿DE，CF折起，使A，B两点重合与点G，得到多面体CDEFG．
（1）求证：平面DEG⊥平面CFG；
（2）求多面体CDEFG的体积．

查看习题详情和答案>>

（2010•济南二模）在△ABC中，∠ACB=90°，∠BAC=30°，AB的垂直平分线分别交AB，AC于D、E（图一），沿DE将△ADE折起，使得平面ADE⊥平面BDEC（图二）．

（1）若F是AB的中点，求证：CF∥平面ADE．
（2）P是AC上任意一点，求证：平面ACD⊥平面PBE．
（3）P是AC上一点，且AC⊥平面PBE，求二面角P-BE-C的大小．

查看习题详情和答案>>

如图是某三棱柱被削去一个底面后的直观图与侧视图、俯视图．已知CF=2AD，侧视图是边长为2的等边三角形；俯视图是直角梯形，有关数据如图所示．
（Ⅰ）求该几何体的体积；
（Ⅱ）求二面角B-DE-F的余弦值．

查看习题详情和答案>>