(1)平面内两条直线的位置关系有三种:重合、平行、相交.
 当直线不平行于坐标轴时,直线与圆的位置关系可根据下表判定
当直线不平行于坐标轴时,直线与圆的位置关系可根据下表判定
|
|
斜截式 |
一般式 |
|
方 程 |
 : :  : : |
 : :  : : |
|
相 交 |
 |
 |
|
垂 直 |
 |
 |
|
平 行 |
 且 且 |
 或 或 |
|
重 合 |
 且 且 |
  |
 当直线平行于坐标轴时可结合图形进行考虑其位置关系.
当直线平行于坐标轴时可结合图形进行考虑其位置关系.
说明:由于直线 的方向向量为
的方向向量为 ,可推导上述结论.
,可推导上述结论.
(2)点到直线的距离、直线与直线的距离:
 点
点 到直线
到直线 的距离为:
的距离为:

 直线
直线 ,且其方程分别为
,且其方程分别为 :
: ,
, :
:
则 与
与 的距离为:
的距离为:

(3)两条直线的夹角公式:若直线 的斜率为
的斜率为 ,
, 的斜率为
的斜率为 ,则:
,则:
 直线
直线 到
到 的角满足:tan
的角满足:tan .
.
 直线
直线 与直线
与直线 所成的角(简称夹角)
所成的角(简称夹角) 满足:
满足:
说明:①当 和
和 的斜率都不存在时,所成的角为
的斜率都不存在时,所成的角为 ;②当
;②当 与
与 的斜率有一个存在时,可画图、观察,根据另一条直线的斜率得出所求的角;③
的斜率有一个存在时,可画图、观察,根据另一条直线的斜率得出所求的角;③  到
到 的角
的角 不同于
不同于 到
到 的角
的角 ,它们满足:
,它们满足: .④到角范围:
.④到角范围: ;夹角范围:
;夹角范围:
(4)两条直线的交点:两条直线的交点的个数取决于这两条直线的方程组成的方程组的解的个数.
 倾斜角:一条直线
倾斜角:一条直线 向上的方向与
向上的方向与 轴的正方向所成的最小正角,叫做直线的倾斜角,范围为
轴的正方向所成的最小正角,叫做直线的倾斜角,范围为 .
.
斜率:当直线的倾斜角不是 时,则称其正切值为该直线的斜率,即
时,则称其正切值为该直线的斜率,即 ;当直线的倾斜角等于
;当直线的倾斜角等于 时,直线的斜率不存在。
时,直线的斜率不存在。
 过两点
过两点 ,
,
 的直线的斜率公式:
的直线的斜率公式:
若 ,则直线
,则直线 的斜率不存在,此时直线的倾斜角为
的斜率不存在,此时直线的倾斜角为 .
.
 (课本
(课本 )直线的方向向量:设
)直线的方向向量:设 为直线上的两点,则向量
为直线上的两点,则向量 及与它平行的向量都
及与它平行的向量都
称为直线的方向向量.若 ,
, ,则直线的方向向量为
,则直线的方向向量为 =
= .
.
直线 的方向向量为
的方向向量为 .当
.当 时,
时, 也为直线的一个方向向量.
也为直线的一个方向向量.
 直线方程的种形式:
直线方程的种形式:
|
名称 |
方程 |
适用范围 |
|
斜截式 |
 |
不含垂直于 轴的直线 轴的直线 |
|
点斜式 |
 |
不含直线 |
|
两点式 |
 |
不含直线 ( ( )和 )和直线   |
|
截距式 |
 |
不含垂直于坐标轴和过原点的直线 |
|
一般式 |
  |
平面直角坐标系内的直线都适用 |
 和
和 ,求满足下列条件的
,求满足下列条件的 值:
值:
 ,且过点
,且过点

 ,底边所在的直线
,底边所在的直线 ,点
,点 在另一腰上,求这腰所在直线
在另一腰上,求这腰所在直线 。直线
。直线 .
.  的值;
的值; 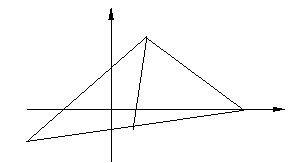 问题4.如图所示,
问题4.如图所示, 的顶点
的顶点 ,
, ,求
,求 的平分线
的平分线 (
( 全国)直线
全国)直线
 的倾斜角为
的倾斜角为



 的倾斜角为
的倾斜角为 ,且
,且 ,则
,则


 共线,则
共线,则 的值等于
的值等于  ,从
,从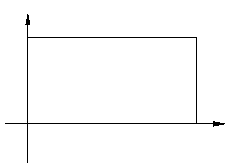
 的长
的长 ,宽为
,宽为 ,
, 、
、 边分别在
边分别在 轴的正半轴上,
轴的正半轴上, 点与坐标原点重合(如图所示).将矩形折叠,使
点与坐标原点重合(如图所示).将矩形折叠,使 上.(Ⅰ)若折痕所在直线的斜率为
上.(Ⅰ)若折痕所在直线的斜率为 ,
,
 的倾斜角为
的倾斜角为
 的斜率分别为
的斜率分别为 ,则
,则
 ,直线
,直线


 ,则
,则


 ,则直线
,则直线 的倾斜角为
的倾斜角为






 表示;
表示; 的直线都可以用方程
的直线都可以用方程 、
、 共线,则
共线,则 在两条坐标轴上的截距绝对值相等的直线条数有
在两条坐标轴上的截距绝对值相等的直线条数有
 的倾斜角为
的倾斜角为
 ,则此直线方程是
,则此直线方程是
 ,
, 的一半,求直线
的一半,求直线 ,求直线
,求直线 ,
, .
. 求直线
求直线 求直线
求直线 若实数
若实数 ,求
,求 ,
, 的值域.
的值域. ,且以
,且以 为方向向量;
为方向向量; 的倾斜角的
的倾斜角的 .
. 面积最小值时
面积最小值时 (
( 重庆) 设数列
重庆) 设数列 满足
满足 ,
, ,(
,( ,…).
,…). 证明
证明 对一切正整数
对一切正整数 成立;
成立; 令
令 ,判断
,判断 的大小,并说明理由 .
的大小,并说明理由 . 的前
的前 满足
满足 ,
, .
. ,
, ,
, 证明:对任意的整数
证明:对任意的整数 ,有
,有 .
. 江苏)设数列
江苏)设数列 项和为
项和为 ,已知
,已知 ,且
,且 ,
, 其中
其中 为常数.
为常数. 与
与 对任何正整数
对任何正整数 都成立.
都成立. 数列
数列 的通项公式是
的通项公式是 ,数列
,数列 第
第 项
项  已知
已知 ,且满足
,且满足 ,则
,则 的最小值为
的最小值为 
 满足
满足
 ,则
,则 的最大值是
的最大值是


 ,
, ,
, ,则
,则 的取值范围是
的取值范围是


 是大于
是大于 的常数,则当
的常数,则当 时,函数
时,函数 的最小值为
的最小值为  ,且
,且 ,
, ,求
,求 的范围
的范围 在
在 有意义,求
有意义,求 的直角三角形面积的最大值为
.
的直角三角形面积的最大值为
. ,
, 且
且 恒成立,则
恒成立,则 的最大值为
的最大值为
 (
( 始终平分圆
始终平分圆 的周长,则
的周长,则 的最小值为
的最小值为 

 的解集为
的解集为 ,求正实数
,求正实数 ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是
 ≥
≥ 的两根都大于
的两根都大于
 ,把几块这样的玻璃板重叠起来,能使通过它们的光线强度在原强度的
,把几块这样的玻璃板重叠起来,能使通过它们的光线强度在原强度的 以下.
以下. .
.
 在
在 上恒成立,求实数
上恒成立,求实数 上的值域是
上的值域是 ,求实数
,求实数
 ,求方程
,求方程 的解;
的解; 上有两个解
上有两个解 ,求
,求
 的解集为空集,求实数
的解集为空集,求实数
 ,当
,当 ≤
≤ ≤
≤ ≤
≤ ≤
≤ 和
和 的解集依次为
的解集依次为 的实数
的实数 在
在 有实数解,求实数
有实数解,求实数 (
( ).
). ≤
≤ 成立.
成立. 与
与 (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度
 (
( 安徽)若对任意
安徽)若对任意 ,不等式
,不等式 ≥
≥ 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是



 上的任意
上的任意 ,
, 恒成立”的只有
恒成立”的只有


 ≥
≥ 上恒成立,求实数
上恒成立,求实数 ,函数
,函数 有最大值,则不等式
有最大值,则不等式 的解集为
的解集为
 .
. 解不等式
解不等式 ;
; 求函数
求函数 的最小值.
的最小值. 的解集为
的解集为 ,不等式
,不等式 ≤
≤ .
. ,求
,求 ,求正数
,求正数