摘要:倾斜角:一条直线向上的方向与轴的正方向所成的最小正角.叫做直线的倾斜角.范围为. 斜率:当直线的倾斜角不是时.则称其正切值为该直线的斜率.即;当直线的倾斜角等于时.直线的斜率不存在. 过两点,的直线的斜率公式: 若.则直线的斜率不存在.此时直线的倾斜角为. (课本)直线的方向向量:设为直线上的两点.则向量及与它平行的向量都 称为直线的方向向量.若..则直线的方向向量为=. 直线的方向向量为.当时.也为直线的一个方向向量. 直线方程的种形式: 名称 方程 适用范围 斜截式 不含垂直于轴的直线 点斜式 不含直线 两点式 不含直线()和 直线 截距式 不含垂直于坐标轴和过原点的直线 一般式 平面直角坐标系内的直线都适用
网址:http://m.1010jiajiao.com/timu_id_4389635[举报]
过抛物线C: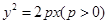 上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
(1)求抛物线C的方程及点M的坐标;
(2)过点M作倾斜角互补的两条直线分别与抛物线C交于A,B两点,如果点M在直线AB的上方,求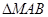 面积的最大值.
面积的最大值.
过抛物线C: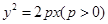 上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
(1)求抛物线C的方程及点M的坐标;
(2)过点M作倾斜角互补的两条直线分别与抛物线C交于A,B两点,且直线AB过点(0,-1),求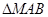 的面积.
的面积.
过抛物线C: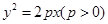 上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
(1)求抛物线C的方程及点M的坐标;
(2)过点M作倾斜角互补的两条直线分别与抛物线C交于A,B两点,如果点M在直线AB的上方,求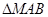 面积的最大值.
面积的最大值.
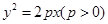 上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.(1)求抛物线C的方程及点M的坐标;
(2)过点M作倾斜角互补的两条直线分别与抛物线C交于A,B两点,如果点M在直线AB的上方,求
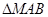 面积的最大值.
面积的最大值.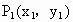 ,
, 两点,则直线l的斜率
两点,则直线l的斜率 ;
; .
.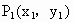 ,
, 两点,则直线l的斜率
两点,则直线l的斜率 ;
;
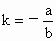 .
.