9.已知抛物线C:y2=4(x-1),椭圆C1的左焦点及左准线与抛物线C的焦点F和准线l分别重合.
(1)设B是椭圆C1短轴的一个端点,线段BF的中点为P,求点P的轨迹C2的方程;
(2)如果直线x+y=m与曲线C2相交于不同两点M、N,求m的取值范围.
(1)解法一:由y2=4(x-1)知抛物线C的焦点F坐标为(2,0).准线l的方程为x=0.设动椭圆C1的短轴的一个端点B的坐标为(x1,y1)(x1>2,y1≠0),点P(x,y),
|
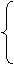
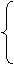
|
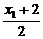 , x1=2x-2,
, x1=2x-2,
y= ,
y1=2y.
,
y1=2y.
∴B(2x-2,2y)(x>2,y≠0).
设点B在准线x=0上的射影为点B′,椭圆的中心为点O′,则椭圆离心率e=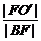 ,由
,由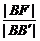 =
=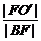 ,得
,得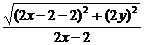 =
=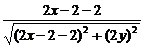 ,
,
整理,化简得y2=x-2(y≠0),这就是点P的轨迹方程.
解法二:抛物线y2=4(x-1)焦点为F(2,0),准线l:x=0.设P(x,y),
∵P为BF中点,
∴B(2x-2,2y)(x>2,y≠0).设椭圆C1的长半轴、短半轴、半焦距分别为a、b、c,
则c=(2x-2)-2=2x-4,b2=(2y)2=4y2,
∵(-c)-(-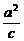 )=2,
)=2,
∴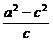 =2,
=2,
即b2=2c.∴4y2=2(2x-4),
即y2=x-2(y≠0),此即C2的轨迹方程.
|
|
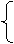 x+y=m,
x+y=m,
y2=x-2
m>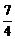 .
.
而当m=2时,直线x+y=2过点(2,0),这时它与曲线C2只有一个交点,
∴所求m的取值范围是(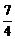 ,2)∪(2,+∞).
,2)∪(2,+∞).
7. 正方形ABCD中,一条边AB在直线y=x+4上,另外两顶点C、D在抛物线y2=x上,求正方形的面积.
解:设CD所在直线的方程为y=x+t,
|
|
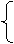 y=x+t,
y=x+t,
y2=x,
x2+(2t-1)x+t2=0,
∴|CD|=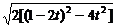
=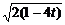 .
.
又直线AB与CD间距离为|AD|=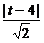 ,
,
∵|AD|=|CD|,
∴t=-2或-6.
从而边长为3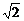 或5
或5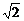 .
.
面积S1=(3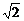 )2=18,S2=(5
)2=18,S2=(5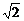 )2=50.
)2=50.
5.设直线l与椭圆交于P1(x1,y1)、P2(x2,y2),
将P1、P2两点坐标代入椭圆方程相减得直线l斜率
k=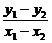 =-
=-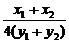 = -
= -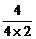 =-
=-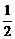 .
.
由点斜式可得l的方程为x+2y-8=0.
答案:x+2y-8=0
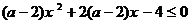 对一切
对一切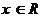 恒成立,则
恒成立,则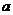 的取值范围是 ( )
的取值范围是 ( )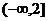 B.
B.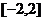 C.
C.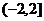 D.
D.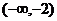
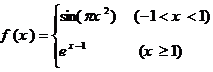 ,若
,若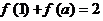 ,则
,则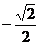 C.
C.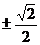 D. 1或
D. 1或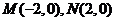 ,动点
,动点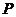 满足条件
满足条件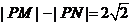 .记动点
.记动点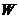 .
. 是
是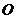 是坐标原点,求
是坐标原点,求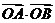 的最小值.
的最小值.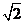 知动点P的轨迹是以M,N为焦点的双曲线的右支,实半轴长a=
知动点P的轨迹是以M,N为焦点的双曲线的右支,实半轴长a=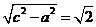 ,
,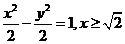
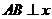 轴时,
轴时,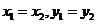 ,从而
,从而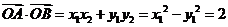 。
。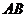 与
与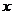 轴不垂直时,设直线
轴不垂直时,设直线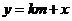 ,与
,与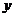 得
得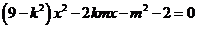 ,
,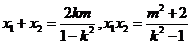
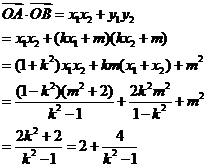
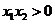 ,所以
,所以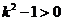 ,从而
,从而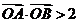 .
.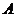 、
、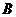 的坐标分别为
的坐标分别为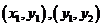 ,则
,则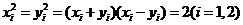
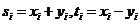 ,
, 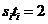 ,且
,且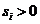 ,
,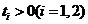 ,所以
,所以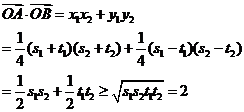
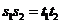 ,即
,即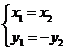 时“=”成立.
时“=”成立.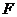 为双曲线
为双曲线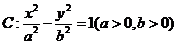 的右焦点,
的右焦点,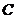 右支上一点,且位于
右支上一点,且位于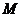 为左准线上一点,
为左准线上一点,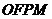 为平行四边形,
为平行四边形,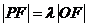 。
。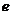 与
与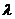 的关系式;
的关系式;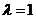 时,经过焦点
时,经过焦点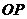 的直线交双曲线于
的直线交双曲线于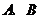 两点,若
两点,若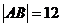 ,求此时的双曲线方程。
,求此时的双曲线方程。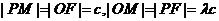
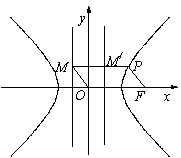

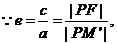
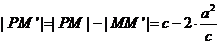
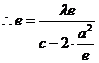
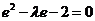
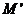 为
为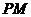 与双曲线右准线的交点,N为左准线与x轴的交点.
与双曲线右准线的交点,N为左准线与x轴的交点.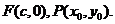 由于
由于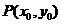 在双曲线右支上,则
在双曲线右支上,则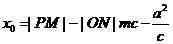 ①
①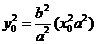 ②
②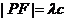 得
得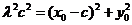 ③
③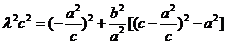
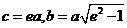 代入上式,得
代入上式,得
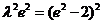 ④
④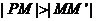
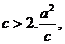 即
即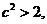 又
又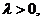 所以由④式得
所以由④式得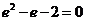 解得
解得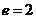
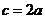 ,
,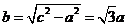
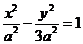
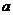 的值
的值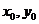 ),则
),则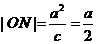 ,
,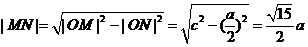
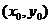 在双曲线的右支上,且位于x轴上方,因而
在双曲线的右支上,且位于x轴上方,因而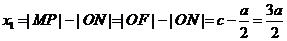 ,
,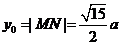
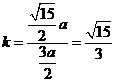
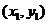 、B
、B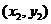 ,则
,则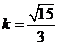 ,直线AB的方程为
,直线AB的方程为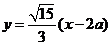
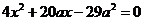
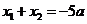 ,
,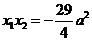
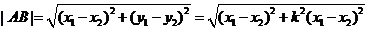
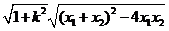
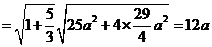
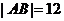 得
得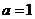 ,于是,所求双曲线得方程为
,于是,所求双曲线得方程为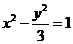
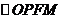 为菱形,其对角线OP与FM互相垂直平分,
为菱形,其对角线OP与FM互相垂直平分,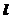 与抛物线
与抛物线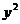 =2
=2
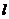 过点T(3,0),那么
过点T(3,0),那么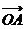
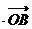 =3”是真命题;
=3”是真命题;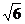 )、B(3,-
)、B(3,-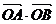 =3;
=3;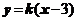 ,其中
,其中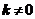 ,
,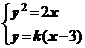 得
得 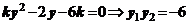
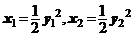 ,
,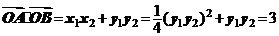 ,
,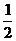 ,1),此时
,1),此时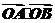 =3,
=3,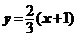 ,而T(3,0)不在直线AB上;
,而T(3,0)不在直线AB上;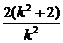 ,
,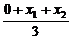 =2.
=2.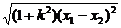 =8, 得k2=1…..
=8, 得k2=1…..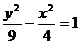 的渐近线为:
的渐近线为: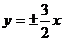 ,而直线y=x+3的斜率为1,1<3/2,因此直线与双曲线的下支有一交点,又y=x+3过椭圆
,而直线y=x+3的斜率为1,1<3/2,因此直线与双曲线的下支有一交点,又y=x+3过椭圆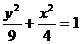 的顶点,k=1>0因此直线与椭圆左半部分有一交点,共计3个交点,选D
的顶点,k=1>0因此直线与椭圆左半部分有一交点,共计3个交点,选D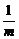 ≤1且m>0,得m≥1.故本题应选C.
≤1且m>0,得m≥1.故本题应选C.