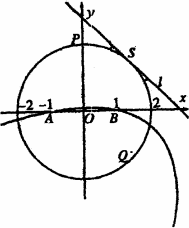
摘要：9．已知抛物线C:y2=4(x-1).椭圆C1的左焦点及左准线与抛物线C的焦点F和准线l分别重合． (1)设B是椭圆C1短轴的一个端点.线段BF的中点为P.求点P的轨迹C2的方程, (2)如果直线x+y=m与曲线C2相交于不同两点M.N.求m的取值范围． (1)解法一:由y2=4(x-1)知抛物线C的焦点F坐标为(2.0)．准线l的方程为x=0．设动椭圆C1的短轴的一个端点B的坐标为(x1.y1)(x1＞2.y1≠0).点P(x.y). ∴ 则 x=. x1=2x-2. y=. y1=2y． ∴B(2x-2.2y)(x＞2.y≠0)． 设点B在准线x=0上的射影为点B′.椭圆的中心为点O′.则椭圆离心率e=.由=.得=. 整理.化简得y2=x-2(y≠0).这就是点P的轨迹方程． 解法二:抛物线y2=4(x-1)焦点为F(2.0).准线l:x=0．设P(x.y). ∵P为BF中点. ∴B(2x-2.2y)(x＞2.y≠0)．设椭圆C1的长半轴.短半轴.半焦距分别为a.b.c. 则c=(2x-2)-2=2x-4.b2=(2y)2=4y2. ∵(-c)-(-)=2. ∴=2. 即b2=2c．∴4y2=2(2x-4). 即y2=x-2(y≠0).此即C2的轨迹方程． (y≠0).得y2+y-m+2=0.令Δ=1-4(-m+2)＞0.解得 (2)解:由 x+y=m. y2=x-2 m＞． 而当m=2时.直线x+y=2过点(2.0).这时它与曲线C2只有一个交点. ∴所求m的取值范围是(.2)∪．

网址：http://m.1010jiajiao.com/timu_id_4044437[举报]