1(汉沽一中2008~2009届月考文16).(本小题满分12分)将 、
、 两枚骰子各抛掷一次,观察向上的点数,问:
两枚骰子各抛掷一次,观察向上的点数,问:
(1)共有多少种不同的结果?
(2)两数之和是3的倍数的结果有多少种?
(3)两数之和是3的倍数的概率是多少?
解:(1)共有 种结果;
……………………………………4分
种结果;
……………………………………4分
(2)共有12种结果; ……………………………………8分
(3) .
………………………………………12分
.
………………………………………12分
2(2009年滨海新区五所重点学校联考理18).(本题满分12分)甲、乙两人进行摸球游戏,一袋中装有2个黑球和1个红球。规则如下:若一方摸中红球,将此球放入袋中,此人继续摸球;若一方没有摸到红球,将摸到的球放入袋中,则由对方摸彩球。现甲进行第一次摸球。
(Ⅰ)在前三次摸球中,甲恰好摸中一次红球的所有情况;
(Ⅱ)在前四次摸球中,甲恰好摸中两次红球的概率。;
(Ⅲ)设 是前三次摸球中,甲摸到的红球的次数,
是前三次摸球中,甲摸到的红球的次数,
求随机变量 的概率分布与期望。
的概率分布与期望。
解: (Ⅰ) 甲红甲黑乙红黑均可;甲黑乙黑甲红。。。。。。。。。。2分
(Ⅱ) 。。。。。。。。。。。。。。。6分
。。。。。。。。。。。。。。。6分
(Ⅲ) 设 的分布是 。。。。。。。。。每求对一个1分共4分,表1分, E
的分布是 。。。。。。。。。每求对一个1分共4分,表1分, E 1分共6分
1分共6分
 |
0 |
1 |
2 |
3 |
|
P |
 |
 |
 |
 |
E =
= 。。。。。。。。。。。。。。。12分
。。。。。。。。。。。。。。。12分
3(2009年滨海新区五所重点学校联考文18).(本小题满分12分)某商场举行抽奖活动,从装有编号0,1,2,3四个小球的抽奖箱中,每次取出后放回,连续取两次,取出的两个小球号码相加之和等于5中一等奖,等于4中二等奖,等于3中三等奖.
(Ⅰ)求中三等奖的概率;
(Ⅱ)求中奖的概率.
解: 设“中三等奖”的事件为A,“中奖”的事件为B,从四个小球中有放回的取两个共有
(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(1,3),(2,0),
(2,1),(2,2),(2,3),(3,0),(3,1),(3,2),(3,3)16种不同的方法。…3分
(Ⅰ)两个小球号码相加之和等于3的取法有4种:
(0,3)、(1,2)、(2,1)、(3,0)…………………4分
故  ……………………………………6分
……………………………………6分
(Ⅱ)两个小球号码相加之和等于3的取法有4种。
两个小球相加之和等于4的取法有3种:(1,3),(2,2),(3,1)
两个小球号码相加之和等于5的取法有2种:(2,3),(3,2), ………………9分
由互斥事件的加法公式得
 ………………12分
………………12分
4(汉沽一中2008~2009届月考理 16).(本小题满分12分)
16).(本小题满分12分)
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中,将3次遇到黑色障碍物,最后落入 袋或
袋或 袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是
袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是 .
.
(Ⅰ)求小球落入 袋中的概率
袋中的概率 ;
;
(Ⅱ)在容器入口处依次放入4个小球,记 为落入
为落入
袋中小球的个数,试求 的概率和
的概率和 的数学期望
的数学期望 .
.
解: (Ⅰ)解法一:记小球落入 袋中的概率
袋中的概率 ,则
,则 ,
,
由于小球每次遇到黑色障碍物时一直向左或者一直向右下落,小球将落入 袋,所以
袋,所以 ‘…………………………………………………………………
2分
‘…………………………………………………………………
2分
 . ……………………………………………………………… 5分
. ……………………………………………………………… 5分
解法二:由于小球每次遇到黑色障碍物时,有一次向左和两次向右或两次向左和一次向右下落时小球将落入 袋.
袋.
 ,
……………………………… 5分
,
……………………………… 5分
(Ⅱ)由题意, 所以有 ……………………………………………… 7分
所以有 ……………………………………………… 7分
 ,
……………………………………… 10分
,
……………………………………… 10分
 .
……………………………… 12分
.
……………………………… 12分
5(汉沽一中2008~2009届月考文16)、(本小题满分12分)
某班甲、乙两学生的高考备考成绩如下:
甲: 512 554 528 549 536 556 534 541 522 538
乙:515 558 521 543 532 559 536 548 527 531
(1)用茎叶图表示两学生的成绩;
(2)分别求两学生成绩的中位数和平均分.
[命题意图]本题主要考查茎叶图、中位数和平均分以及考查学生对数据的处理能力.
[解析](1)两学生成绩绩的茎叶图如图所示 :……6分
 (2)将甲、乙两学生的成绩从小到大排列为:
(2)将甲、乙两学生的成绩从小到大排列为:
甲: 512 522 528 534 536 538 541 549 554 556
……7分
乙:515 521 527 531 532 536 543 548 558 559
……8分
从以上排列可知甲学生成绩的中位数为 ……9分
……9分
乙学生成绩的中位数为 ……10分
……10分
甲学生成绩的平均数为:
 ……11分
……11分
乙学生成绩的平均数为:
 ……12分
……12分
6(汉沽一中2008~2009届月考文17)、(本小题满分14分)
某射手在一次射击中命中9环的概率是0.28,命中8环的概率是0.19,不够8环的概率是0.29,计算这个射手在一次射击中命中9环或10环(最高环数)的概率.
17[命题意图]本题主要考查互斥事件、对立事件、概率的基本性质以及考查学生用概念和公式规范解题的能力.
[解析]记这个射手在一次射击中“命中10环或9环”为事件A,“命中10环、9环、8环、不够8环”分别记为B、C、D、E. ……1分
则 ,
, ,
, ……2分
……2分
∵C、D、E彼此互斥, ……3分
∴P(C∪D∪E)=P(C)+P(D)+P(E)=0.28+0.19+0.29=0.76. ……7分
又∵B与C∪D∪E为对立事件, ……8分
∴P(B)=1-P(C∪D∪E)=1-0.76=0.24. ……10分
B与C互斥,且A=B∪C, ……11分
∴P(A)=P(B+C)=P(B)+P(C) =0.24+0.28=0.52. ……13分
答:某射手在一次射击中命中9环或10环(最高环数)的概率为0.52. ……14分
7(汉沽一中2008~2008学年月考理15).(本小题满分13分)
学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人.设 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且 .
.
(I) 求文娱队的人数;
(II) 写出 的概率分布列并计算
的概率分布列并计算 .
.
解:设既会唱歌又会跳舞的有x人,则文娱队中共有(7-x)人,那么只会一项的人数是
(7-2 x)人.
(I)∵ ,
,
∴ .……………………………………3分
.……………………………………3分
即 .
.
∴ .
.
∴x=2. ……………………………………5分
故文娱队共有5人.……………………………………7分
(II)  的概率分布列为
的概率分布列为
 |
0 |
1 |
2 |
|
P |
 |
 |
 |
 ,……………………………………9分
,……………………………………9分
 ,……………………………………11分
,……………………………………11分
∴ =1. …………………………13分
=1. …………………………13分
8(和平区2008年高考数学(文)三模18). (本小题满分12分)
有甲、乙、丙三种产品,每种产品的测试合格率分别为0.8,0.8和0.6,从三种产品中各抽取一件进行检验。
(1)求恰有两件合格的概率;
(2)求至少有两件不合格的概率。
解:(1)设从甲、乙、丙三种产品中各抽出一件测试为事件A,B,C,由已知P(A)=0.8,P(B)=0.8,P(C)=0.6
则恰有两件产品合格的概率为

 (6分)
(6分)
(2)三件产品均测试合格的概率为
 (8分)
(8分)
由(1)知,恰有一件测试不合格的概率为
 (10分)
(10分)
所以至少有两件不合格的概率为
 (12分)
(12分)
9(和平区2008年高考数学(理)三模18). (本小题满分12分)
有一批数量很大的产品,其次品率是10%。
(1)连续抽取两件产品,求两件产品均为正品的概率;
(2)对这批产品进行抽查,每次抽出一件,如果抽出次品,则抽查终止,否则继续抽查,直到抽出次品,但抽查次数最多不超过4次,求抽查次数 的分布列及期望。
的分布列及期望。
18. (本小题满分12分)
解:(1)两件产品均为正品的概率为
 (3分)
(3分)
(2) 可能取值为1,2,3,4
可能取值为1,2,3,4
 ;
; ;
;
 (9分)
(9分)
所以次数 的分布列如下
的分布列如下
 (10分)
(10分)
∴  (12分)
(12分)
 的方程
的方程
 且
且 ,求实数m的值;
,求实数m的值;
 。
4分
。
4分 。过圆心C作直线L的垂线CD,D为垂足。
。过圆心C作直线L的垂线CD,D为垂足。
 又由
又由 6分
6分 。
。 ,
, 

 和
和 10分
10分 ,
,

 。
12分
。
12分 与直线
与直线 的交点个数是__ 。2
的交点个数是__ 。2
 2(2009年滨海新区五所重点学校联考理12).已知圆O直径为10,AB是圆O的直径,C为圆O上一点,且BC=6,
2(2009年滨海新区五所重点学校联考理12).已知圆O直径为10,AB是圆O的直径,C为圆O上一点,且BC=6,  被直线
被直线 截得的弦长为
截得的弦长为 ,则
,则  = .
= .
 相切的直线方程是 .16x-8y+25=0
相切的直线方程是 .16x-8y+25=0 的圆心与点
的圆心与点 关于直线
关于直线 对称.直
对称.直 与圆
与圆 两点,且
两点,且 ,则圆
,则圆
 ”是“直线
”是“直线 平行于直线
平行于直线 ”的
( C )
”的
( C ) (一中2008-2009月考理3).从点
(一中2008-2009月考理3).从点 向圆
向圆 引切线,则一条切线长的最小值为
( A )
引切线,则一条切线长的最小值为
( A ) B.5 C.
B.5 C. D.
D.
 上,当圆心到直线
上,当圆心到直线 的距离最少时,该圆的方程为( A
)
的距离最少时,该圆的方程为( A
) 或
或


 或
或
 和圆
和圆 关于直线
关于直线 对称,动圆P与圆C相外切且与直线
对称,动圆P与圆C相外切且与直线 相切,则动圆P的圆心的轨迹方程是(C )
相切,则动圆P的圆心的轨迹方程是(C ) B.
B.

 D.
D.

 B.
B.
 (x > 0) D.
(x > 0) D.
 9(汉沽一中2008~2009届月考理
8).如右图,已知
9(汉沽一中2008~2009届月考理
8).如右图,已知 ,从点
,从点 射出的光线经直线
射出的光线经直线 反射后再射到直线
反射后再射到直线 上,最后经直线
上,最后经直线 点,则光线所经过的路程是(A)
点,则光线所经过的路程是(A)



 所高校中的
所高校中的 所学校的自主招生考试,由于其中两所学校的考试时间相同,因此,该学生不能同时报考这两所学校.则该学生不同的报名方法种数是
.(用数字作答) 16 .
所学校的自主招生考试,由于其中两所学校的考试时间相同,因此,该学生不能同时报考这两所学校.则该学生不同的报名方法种数是
.(用数字作答) 16 .  ,
, ,
, 由此得到频率分布直方图如下图,则这20名工人中一天生产该产品数量在
由此得到频率分布直方图如下图,则这20名工人中一天生产该产品数量在 的人数是 .
的人数是 .
 内随机地抽取两数
内随机地抽取两数 则满足
则满足 概率是
概率是 ;
; ,l2:x- by + 1= 0,则
,l2:x- by + 1= 0,则 的充要条件是
的充要条件是 ;
; ③为了解一片经济林的生长情况,随机测量了其中100株树木的底部周长(单位:cm)。根据所得数据画出样本的频率分布直方图(如右),那么在这100株树木中,底部周长小于110cm的株数是70株;
③为了解一片经济林的生长情况,随机测量了其中100株树木的底部周长(单位:cm)。根据所得数据画出样本的频率分布直方图(如右),那么在这100株树木中,底部周长小于110cm的株数是70株; 的中心
的中心 与点
与点
 的距离为
的距离为 .
. B.
B. C.
C. D.
D.
 (汉沽一中2008~2009届月考文2).
要从其中有50个红球的1000个形状相同的球中,采用按颜色分层抽样的方法抽取100个进行分析,则应抽取红球的个数为(A )
(汉沽一中2008~2009届月考文2).
要从其中有50个红球的1000个形状相同的球中,采用按颜色分层抽样的方法抽取100个进行分析,则应抽取红球的个数为(A ) ,则
,则

 时,
时,
 ∵
∵
 ∴
∴


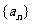 是等比数列(2分)
是等比数列(2分) ∴
∴
 即
即
 (4分)
(4分) 在直线
在直线 上
上 ∴
∴

 是等差数列,又
是等差数列,又 ∴
∴  (6分)
(6分)
 ①(7分)
①(7分) ②
②

 (10分)
(10分) 即
即
 (11分)
(11分) 时,
时, (12分)
(12分) 时,
时, (13分)
(13分) .
. ,又
,又 ∴
∴ 
 ,所以
,所以 (2分)
(2分) 的等差数列(3分)
的等差数列(3分) 时,
时, ,所以
,所以 (4分)
(4分) ,又
,又 ∴
∴ 
 是公比为
是公比为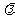 的等比数列(6分)
的等比数列(6分) 时,
时,
 时,
时, (8分)
(8分) ,而
,而 ∴
∴ 
 ①(9分)
①(9分) (10分)
(10分) ②(11分)
②(11分)

 (13分)
(13分) 时,
时, (14分)
(14分)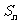 ,且
,且 中,
中,
 2分
2分

 10分
10分
 12分
12分 ,设曲线
,设曲线 在点
在点 处的切线与
处的切线与 轴的交点为
轴的交点为 ,其中
,其中 为正实数
(1)用
为正实数
(1)用 表示
表示 ;
(2)
;
(2) ,若
,若 ,试证明数列
,试证明数列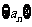 为等比数列,并求数列
为等比数列,并求数列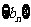 的前
的前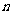 项和
项和 ,记数列
,记数列 的前
的前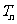 ,求
,求 ,所以在曲线上点
,所以在曲线上点 处的切线方程为
处的切线方程为 ,即
,即 -----------------2分
-----------------2分 ,得
,得 ,即
,即
 ,所以
,所以 -----------------4分
-----------------4分

 ,所以数列
,所以数列 ---8分
---8分  时,
时,
 时,
时,
 ,故数列
,故数列 的通项公式为
的通项公式为
 ①
① 的
的 ②
② ②得
②得
 -----------------14分
-----------------14分


 为非零实常数)
为非零实常数) ,求证数列
,求证数列 ,求证数列
,求证数列 的前n项和
的前n项和 。
。 ,
,
 ,---------------------------------------------------------------------------3分
,---------------------------------------------------------------------------3分
 得
得
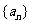 是首项
是首项 的等比数列,∴
的等比数列,∴ ------5分
------5分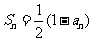 得
得
 ,∴
,∴
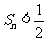 ---------------------------------------------------------9分
---------------------------------------------------------9分 ,
, --------------------------------7分
--------------------------------7分
 =
= -----------10分
-----------10分 -------------------12分
-------------------12分

 =
= --------14分
--------14分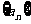 的首项
的首项 ,公差
,公差 ,前
,前 ,
, 的通项公式;
的通项公式;
 等差数列
等差数列
 …………………………4分
…………………………4分 …………………………6分
…………………………6分
 ………8分
………8分 …………10分
…………10分


 .
…………………12分
.
…………………12分 分)
分) 是曲线
是曲线 上的
上的 在
在 是正三角形(
是正三角形( 是坐标原点) .
是坐标原点) . ;
;
 的横坐标
的横坐标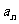 关于
关于 ,若对任意正整数
,若对任意正整数 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. .…………………………………………… 2分
.…………………………………………… 2分 ,则
,则
 ,
, … 3分
… 3分 中,有
中,有 .
. .…………………………………………………… 4分
.…………………………………………………… 4分 ,
, ,
①
,
① .
②
.
②
 ,
, ,
………………………………… 6分
,
………………………………… 6分 .
.  是以
是以 为首项,公差为
为首项,公差为 的等差数列.
的等差数列. , …………………………………… 7分
, …………………………………… 7分
 ,
,
 .
. . ………………………… 8分
. ………………………… 8分 ,
,  .
.

 .
. 时,上式恒为负值,
时,上式恒为负值, ,
, 是递减数列.
是递减数列.
 的最大值为
的最大值为 .
………………………………………………… 11分
.
………………………………………………… 11分 在
在 在
在 ,则
,则 且
且 ,
,
 或
或 ,
, .…………………………………………… 14分
.…………………………………………… 14分



 ,则
,则 .
. 时,
时, ,
, 在
在 是增函数.
是增函数. .
………………………………………………… 11分
.
………………………………………………… 11分 ,
, ,且
,且 ,求
,求 ……4分
……4分 ,满足上式
……6分
,满足上式
……6分 ……7分
……7分 , ∴
, ∴ ……9分
……9分 ……11分
……11分 ……13分
……13分 ……14分
……14分 ,
, ,数列
,数列 满足
满足 ,
, ,
,  .
. 是等比数列;
是等比数列; 取最大值,并求出最大值;
取最大值,并求出最大值; 对任意
对任意 恒成立,求实数
恒成立,求实数
