摘要:解:(Ⅰ)当时 . ∴.---------------------------------------------------------------------------3分 由得 ∴数列是首项.公比为的等比数列.∴------5分 (Ⅱ)证法1: 由得---------------------------------7分 .∴ ∴---------------------------------------------------------9分 知. ∴ --------------------------------7分 .∴---------------------------------8分 即 -------------------------------------------------9分 (Ⅲ) = -----------10分 = -------------------12分 ∵ ∴=--------14分 4(汉沽一中2008~2009届月考文15).已知等差数列的首项.公差.前项和为.. (1)求数列的通项公式, (2)求证: 解:(1)等差数列中.公差 ----------4分 (2) ----------6分 ---8分 ----10分 . -------12分 5(汉沽一中2008~2009届月考理20).(本小题满分分) 如图.是曲线 上的个点.点在轴的正半轴上.是正三角形(是坐标原点) . (Ⅰ) 写出, (Ⅱ)求出点的横坐标关于的表达式, (Ⅲ)设.若对任意正整数.当时.不等式恒成立.求实数的取值范围. 解:(Ⅰ) .----------------- 2分 (Ⅱ)依题意.则 .- 3分 在正三角形中.有 . .-------------------- 4分 . . ① 同理可得 . ② ①-②并变形得 . . ------------- 6分 . ∴数列是以为首项.公差为的等差数列. . -------------- 7分 . . . ---------- 8分 (Ⅲ)解法1 :∵. ∴. . ∴当时.上式恒为负值. ∴当时.. ∴数列是递减数列. 的最大值为. ------------------- 11分 若对任意正整数.当时.不等式恒成立.则不等式在时恒成立.即不等式在时恒成立. 设.则且. ∴ 解之.得 或. 即的取值范围是.----------------- 14分 解法2:∵. 设.则 . 当时.. 在是增函数. ∴数列是递减数列. 的最大值为. ------------------- 11分 (以下解答过程与解法1相同) 6(汉沽一中2008~2009届月考文19). 已知数列{}的前项和, (Ⅰ)求数列的通项公式, (Ⅱ)设,且.求. [命题意图]本题主要是对数列通项和求和公式的综合考查.以及考查学生的分析综合能力和分类讨论的数学思想. [解析](Ⅰ)∵Sn=n2+2n ∴当时. --4分 当n=1时.a1=S1=3. ,满足上式 --6分 故 --7分 (Ⅱ)∵, ∴ --9分 ∴ --11分 ∴ --13分 --14分 7(汉沽一中2008~2008学年月考理19).已知..数列满足. . . (Ⅰ)求证:数列是等比数列, (Ⅱ)当n取何值时.取最大值.并求出最大值, (III)若对任意恒成立.求实数的取值范围. (8(汉沽一中2009届月考文18).在数列中. 且 求的通项公式.
网址:http://m.1010jiajiao.com/timu_id_4004451[举报]
在平行四边形OABC中,已知过点C的直线与线段OA,OB分别相交于点M,N.若
=x
,
=y
.
(1)求证:x与y的关系为y=
;
(2)设f(x)=
,定义函数F(x)=
-1(0<x≤1),点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为
的等比数列,O为原点,令
=
+
+…+
,是否存在点Q(1,m),使得
⊥
?若存在,请求出Q点坐标;若不存在,请说明理由.
(3)设函数G(x)为R上偶函数,当x∈[0,1]时G(x)=f(x),又函数G(x)图象关于直线x=1对称,当方程G(x)=ax+
在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.
查看习题详情和答案>>
| OM |
| OA |
| ON |
| OB |
(1)求证:x与y的关系为y=
| x |
| x+1 |
(2)设f(x)=
| x |
| x+1 |
| 1 |
| f(x) |
| 1 |
| 2 |
| OP |
| OP1 |
| OP2 |
| OPn |
| OP |
| OQ |
(3)设函数G(x)为R上偶函数,当x∈[0,1]时G(x)=f(x),又函数G(x)图象关于直线x=1对称,当方程G(x)=ax+
| 1 |
| 2 |
在平行四边形OABC中,已知过点C的直线与线段OA,OB分别相交于点M,N.若
=x
,
=y
.
(1)求证:x与y的关系为y=
;
(2)设f(x)=
,定义函数F(x)=
-1(0<x≤1),点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为
的等比数列,O为原点,令
=
+
+…+
,是否存在点Q(1,m),使得
⊥
?若存在,请求出Q点坐标;若不存在,请说明理由.
(3)设函数G(x)为R上偶函数,当x∈[0,1]时G(x)=f(x),又函数G(x)图象关于直线x=1对称,当方程G(x)=ax+
在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.
查看习题详情和答案>>
| OM |
| OA |
| ON |
| OB |
(1)求证:x与y的关系为y=
| x |
| x+1 |
(2)设f(x)=
| x |
| x+1 |
| 1 |
| f(x) |
| 1 |
| 2 |
| OP |
| OP1 |
| OP2 |
| OPn |
| OP |
| OQ |
(3)设函数G(x)为R上偶函数,当x∈[0,1]时G(x)=f(x),又函数G(x)图象关于直线x=1对称,当方程G(x)=ax+
| 1 |
| 2 |
在平行四边形OABC中,已知过点C的直线与线段OA,OB分别相交于点M,N.若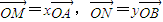 .
.
(1)求证:x与y的关系为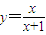 ;
;
(2)设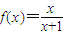 ,定义函数
,定义函数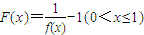 ,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为
,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为 的等比数列,O为原点,令
的等比数列,O为原点,令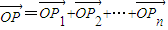 ,是否存在点Q(1,m),使得
,是否存在点Q(1,m),使得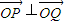 ?若存在,请求出Q点坐标;若不存在,请说明理由.
?若存在,请求出Q点坐标;若不存在,请说明理由.
(3)设函数G(x)为R上偶函数,当x∈[0,1]时G(x)=f(x),又函数G(x)图象关于直线x=1对称,当方程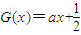 在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.
在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.
查看习题详情和答案>>
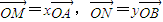 .
.(1)求证:x与y的关系为
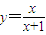 ;
;(2)设
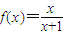 ,定义函数
,定义函数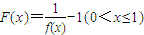 ,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为
,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为 的等比数列,O为原点,令
的等比数列,O为原点,令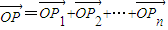 ,是否存在点Q(1,m),使得
,是否存在点Q(1,m),使得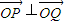 ?若存在,请求出Q点坐标;若不存在,请说明理由.
?若存在,请求出Q点坐标;若不存在,请说明理由.(3)设函数G(x)为R上偶函数,当x∈[0,1]时G(x)=f(x),又函数G(x)图象关于直线x=1对称,当方程
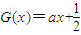 在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.
在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.查看习题详情和答案>>
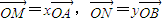 .
.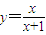 ;
;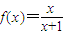 ,定义函数
,定义函数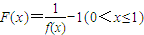 ,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为
,点列Pi(xi,F(xi))(i=1,2,…,n,n≥2)在函数F(x)的图象上,且数列{xn}是以首项为1,公比为 的等比数列,O为原点,令
的等比数列,O为原点,令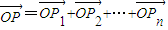 ,是否存在点Q(1,m),使得
,是否存在点Q(1,m),使得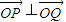 ?若存在,请求出Q点坐标;若不存在,请说明理由.
?若存在,请求出Q点坐标;若不存在,请说明理由.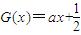 在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.
在x∈[2k,2k+2](k∈N)上有两个不同的实数解时,求实数a的取值范围.