1(汉沽一中2008~2009届月考文19).(本小题满分14分)若函数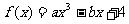 ,当
,当 时,函数
时,函数 有极值
有极值 ,
,
(1)求函数的解析式;
(2)若函数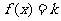 有3个解,求实数
有3个解,求实数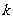 的取值范围.
的取值范围.
解: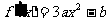 …………………………………………………………2分
…………………………………………………………2分
(1)由题意: …………………………………4分
…………………………………4分
解得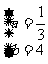 ……………………………………6分
……………………………………6分
 所求解析式为
所求解析式为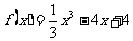
(2)由(1)可得: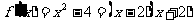
令 ,得
,得 或
或 ………………………………8分
………………………………8分
当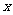 变化时,
变化时, 、
、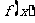 的变化情况如下表:
的变化情况如下表:
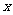 |
 |
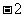 |
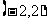 |
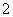 |
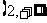 |
 |
 |
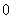 |
- |
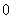 |
 |
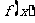 |
单调递增↗ |
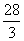 |
单调递减↘ |
 |
单调递增↗ |
因此,当 时,
时,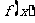 有极大值
有极大值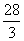 …………………9分
…………………9分
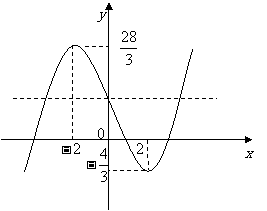 当
当 时,
时,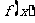 有极小值
有极小值 …………………10分
…………………10分
 函数
函数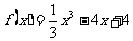 的图象大致如图:……13分
y=k
的图象大致如图:……13分
y=k
由图可知: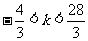 ………………………14分
………………………14分
2(汉沽一中2008~2009届月考理19).(本小题满分14分)
已知 ,
,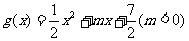 ,直线
,直线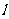 与函数
与函数 、
、 的图象都相切,且与函数
的图象都相切,且与函数 的图象的切点的横坐标为
的图象的切点的横坐标为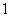 .
.
(Ⅰ)求直线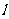 的方程及
的方程及 的值;
的值;
(Ⅱ)若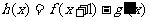 (其中
(其中 是
是 的导函数),求函数
的导函数),求函数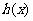 的最大值;
的最大值;
(Ⅲ)当 时,求证:
时,求证: .
.
解:(Ⅰ)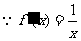 ,
,
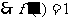 .
.
∴直线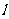 的斜率为
的斜率为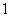 ,且与函数
,且与函数 的图象的切点坐标为
的图象的切点坐标为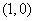 .
.
∴直线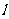 的方程为
的方程为 .
…………………… 2分
.
…………………… 2分
又∵直线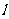 与函数
与函数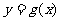 的图象相切,
的图象相切,
∴方程组 有一解.
有一解.
由上述方程消去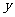 ,并整理得
,并整理得
 ①
①
依题意,方程①有两个相等的实数根,
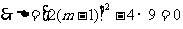
解之,得
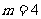 或
或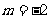

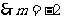 .
…………………… 5分
.
…………………… 5分
(Ⅱ)由(Ⅰ)可知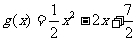 ,
,
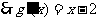
 .
…………………… 6分
.
…………………… 6分
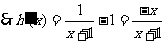 .
…………………… 7分
.
…………………… 7分
∴当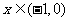 时,
时, ,
,
当 时,
时,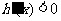 .
.
∴当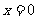 时,
时,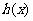 取最大值,其最大值为2. …………………… 10分
取最大值,其最大值为2. …………………… 10分
(Ⅲ)  . ……… 12分
. ……… 12分
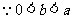 ,
,
 ,
,
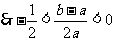 .
.
由(Ⅱ)知当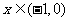 时,
时,
∴当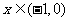 时,
时, ,
,
 .
.
∴ .
………………………………… 14分
.
………………………………… 14分
3(2009年滨海新区五所重点学校联考理)19.(本小题满分12分)
定义在R上的增函数y=f(x)对任意x,y∈R都有f(x+y)=f(x)+f(y).
(Ⅰ)求f(0)
(Ⅱ)求证f(x)为奇函数;
(Ⅲ)若f(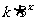 )+f(3
)+f(3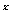 -9
-9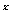 -2)<0对任意x∈R恒成立,求实数k的取值范围.
-2)<0对任意x∈R恒成立,求实数k的取值范围.
19.(本小题满分12分)
解:(Ⅰ)令x=y=0,代入①式,得f(0+0)=f(0)+f(0),即 f(0)=0.………2分
(Ⅱ)令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,则有
0=f(x)+f(-x).即f(-x)=-f(x)对任意x∈R成立,
所以f(x)是奇函数. ………………………………6分
(Ⅲ) 因为f(x)在R上是增函数,又由(Ⅱ)知f(x)是奇函数.
f(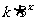 )<-f(3
)<-f(3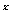 -9
-9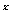 -2)=f(-3
-2)=f(-3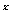 +9
+9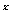 +2),
+2),
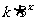 <-3
<-3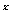 +9
+9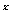 +2,
+2,
3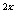 -(1+k)
-(1+k)
 +2>0对任意x∈R成立. …… …………………8分
+2>0对任意x∈R成立. …… …………………8分
令t=3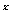 >0,问题等价于t
>0,问题等价于t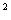 -(1+k)t+2>0对任意t>0恒成立.
-(1+k)t+2>0对任意t>0恒成立.
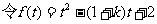 ,其对称轴为
,其对称轴为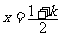
 ………………10分
………………10分
 解得:
解得:
综上所述,当 时,
时,
f(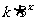 )+f(3
)+f(3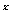 -9
-9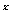 -2)<0对任意x∈R恒成立.…12分
-2)<0对任意x∈R恒成立.…12分
法二:由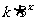 <-3
<-3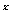 +9
+9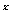 +2………………8分
+2………………8分
得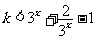 ……………9分
……………9分
 ,即u的最小值为
,即u的最小值为 ,………11分
,………11分
要使对x∈R不等式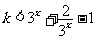 恒成立,只要使
恒成立,只要使 ……12分
……12分
4(和平区2008年高考数学(文)三模)20. (本小题满分12分)
已知函数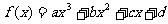 ,
,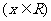 在任意一点
在任意一点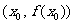 处的切线的斜率为
处的切线的斜率为 。
。
(1)求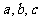 的值;
的值;
(2)求函数 的单调区间;
的单调区间;
(3)若 在
在 上的最小值为
上的最小值为 ,求
,求 在R上的极大值。
在R上的极大值。
解:(1)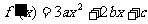 (1分)
(1分)
而 在
在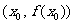 处的切线斜率
处的切线斜率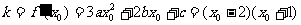
∴ 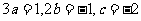 ∴
∴
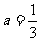 ,
,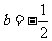 ,
,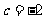 (3分)
(3分)
(2)∵ 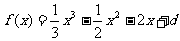
由 知
知 在
在 和
和 上是增函数
上是增函数
由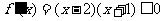 知
知 在
在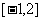 上为减函数(7分)
上为减函数(7分)
(3)由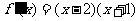 及
及 可列表
可列表
|
x |
 |
 |
 |
 |
+ |
0 |
- |
 |
 |
极大值 |
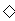 |
 在
在 上的最小值产生于
上的最小值产生于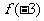 和
和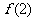
由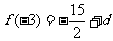 ,
,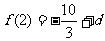 知
知 (9分)
(9分)
于是
则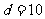 (11分)
(11分)
∴ 
即所求函数 在R上的极大值为
在R上的极大值为 (12分)
(12分)
5(和平区2008年高考数学(理)三模2)0. (本小题满分12分)
已知 ,函数
,函数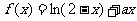 。
。
(1)设曲线 在点
在点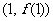 处的切线为
处的切线为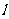 ,若
,若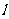 与圆
与圆 相切,求
相切,求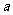 的值;
的值;
(2)求函数 的单调区间;
的单调区间;
(3)求函数 在[0,1]上的最小值。
在[0,1]上的最小值。
解:(1)依题意有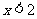 ,
, (1分)
(1分)
过点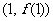 的直线斜率为
的直线斜率为 ,所以过
,所以过 点的直线方程为
点的直线方程为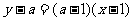 (2分)
(2分)
又已知圆的圆心为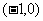 ,半径为1
,半径为1
∴ 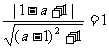 ,解得
,解得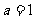 (3分)
(3分)
(2)
当 时,
时, (5分)
(5分)
令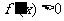 ,解得
,解得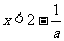 ,令
,令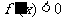 ,解得
,解得
所以 的增区间为
的增区间为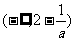 ,减区间是
,减区间是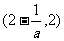 (7分)
(7分)
(3)当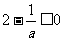 ,即
,即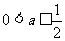 时,
时, 在[0,1]上是减函数
在[0,1]上是减函数
所以 的最小值为
的最小值为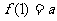 (8分)
(8分)
当 即
即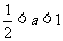 时
时
 在
在 上是增函数,在
上是增函数,在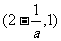 是减函数
是减函数
所以需要比较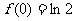 和
和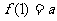 两个值的大小(9分)
两个值的大小(9分)
因为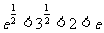 ,所以
,所以
∴ 当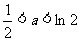 时最小值为
时最小值为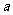 ,当
,当 时,最小值为
时,最小值为 (10分)
(10分)
当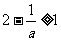 ,即
,即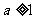 时,
时, 在[0,1]上是增函数
在[0,1]上是增函数
所以最小值为 (11分)
(11分)
综上,当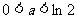 时,
时, 为最小值为
为最小值为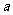
当 时,
时, 的最小值为
的最小值为 (12分)
(12分)
6(2009年滨海新区五所重点学校联考理20).(本小题满分12分)已知 函数
函数
 .
.
(Ⅰ)设曲线 在点
在点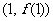 处的切线为
处的切线为 若
若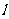 与圆
与圆
相离,求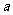 的取值范围;
的取值范围;
(Ⅱ)求函数 在
在 上的最大值.
上的最大值.
解:(Ⅰ) 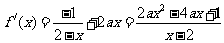 …………2分
…………2分
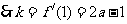 ,切点坐标为(1,
,切点坐标为(1,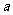 )
………3分
)
………3分
∴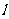 的方程为:y-a=(2a-1)(x-1),即 (2a-1)x-y+(1-a)=0 ……4分
的方程为:y-a=(2a-1)(x-1),即 (2a-1)x-y+(1-a)=0 ……4分
∵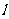 与圆
与圆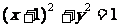 相离
相离
∴由点到直线的距离公式得: ……5分
……5分
注意到 解得:
解得: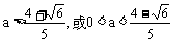 …………6分
…………6分
(Ⅱ) 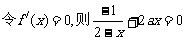 ;
;
有 ,
, 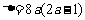 …………7分
…………7分
(1)当 时,
时,
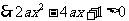 ,
,
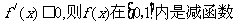 ,
,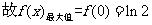 …8分
…8分
(2)当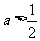 时,
时,
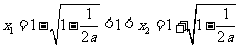
显然,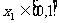 ,列表有:
,列表有:
|
x |
0 |
(0,x1) |
 |
(x1,1) |
1 |
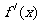 |
|
- |
0 |
+ |
|
 |
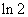 |
↘ |
极小值 |
↗ |
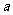 |
……………10分
故:若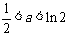 ,则
,则 的最大值为
的最大值为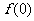 =
=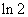 ;
;
若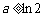 ,则
,则 的最大值为
的最大值为 =
=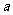 ………………………11分
………………………11分
综上由(1)(2)可知: ……………………12分
……………………12分
7(2009年滨海新区五所重点学校联考文20).(本小题满分12分)已知函数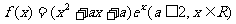
(Ⅰ)当 的单调区间;
的单调区间;
(Ⅱ)是否存在实数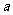 ,使
,使 的极大值为3;若存在,
的极大值为3;若存在,
求出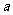 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
解:(Ⅰ)
 …………………………………………3分
…………………………………………3分
当
所以函数的单调增区间为(- ,-2),(-1,+
,-2),(-1,+ );
);
单调减区间为(-2,-1) …………………………6分
(Ⅱ)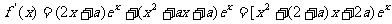

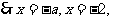 ………………… ………………8分
………………… ………………8分
列表如下: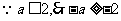 ……………………………………加表格10分
……………………………………加表格10分
|
x |
 |
-2 |
(-2,-a) |
-a |
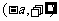 |
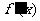 |
+ |
0 |
- |
0 |
+ |
 |
 |
极大 |
 |
极小 |
 |
由表可知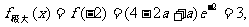 解得
解得 ,所以存在实数a,使
,所以存在实数a,使 的极大值为3。………………………………………………12分
的极大值为3。………………………………………………12分
8(汉沽一中2009届月考文20).(本小题满分12分)
某市旅游部门开发一种旅游纪念品,每件产品的成本是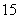 元,销售价是
元,销售价是 元,月平均销售
元,月平均销售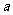 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为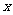
 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是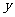 (元).
(元).
(Ⅰ)写出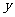 与
与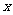 的函数关系式;
的函数关系式;
(Ⅱ)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大.
解: (Ⅰ)改进工艺后,每件产品的销售价为 ,月平均销售量为
,月平均销售量为 件,则月平均利润
件,则月平均利润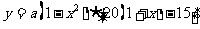 (元),
(元),
∴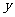 与
与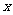 的函数关系式为
的函数关系式为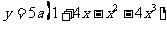
 .…………6分
.…………6分
(Ⅱ)由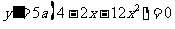 得
得 ,
, (舍), ……………8分
(舍), ……………8分
当 时
时 ;
;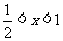 时
时 ,
,
∴函数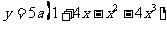
 在
在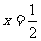 取得最大值.
取得最大值.
故改进工艺后,产品的销售价为
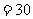 元时,旅游部门销售该纪念品的月平均利
元时,旅游部门销售该纪念品的月平均利
润最大.
9(汉沽一中2009届月考文21)..(本小题满分14分)
已知函数 ,
, ,且
,且 在区间
在区间 上为增函数.
上为增函数.
(1)求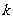 的取值范围;
的取值范围;
(2)若函数 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数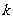 的取值范围.
的取值范围.
.解:(1)由题意 …1分 因为
…1分 因为 上为增函数
上为增函数
所以 在
在 上恒成立 …………………………………………………3分
上恒成立 …………………………………………………3分
即 恒成立,又
恒成立,又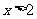 ,所以
,所以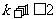 ,故
,故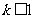
所以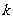 的取值范围为
的取值范围为 ……………………………………………………………………………6分
……………………………………………………………………………6分
(2)设 ,
,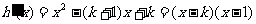
令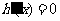 得
得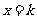 或
或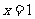 …8分 由(1)知
…8分 由(1)知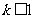
①当 时,
时, 在
在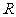 上递增,显然不合题意…………………………………9分
上递增,显然不合题意…………………………………9分
②当 时,
时, 随
随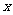 的变化情况如下表:
的变化情况如下表:
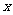 |
 |
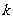 |
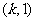 |
1 |
(1,+ ) ) |
||
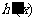 |
+ |
0 |
- |
0 |
|
||
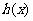 |
↗ |
极大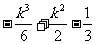 |
↘ |
极小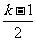 |
↗ |
由于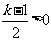 ,欲使
,欲使 图象有三个不同的交点,即方程
图象有三个不同的交点,即方程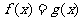 ,也即
,也即 有三个不同的实根故需
有三个不同的实根故需 即
即
 …………………………………12分
…………………………………12分
所以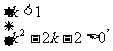 解得
解得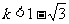 ,综上,所求k的范围为
,综上,所求k的范围为 ……………………14分
……………………14分
10(一中2008-2009月考理21).已知f(x)=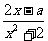 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.
(1)求实数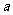 的值组成的集合
的值组成的集合 ;
;
(2) 设关于x的方程f(x)=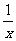 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式
m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
解:(Ⅰ)f'(x)=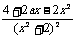 =
= 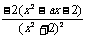 ,∵f(x)在[-1,1]上是增函数,∴f'(x)≥0对x∈[-1,1]恒成立,即x2-ax-2≤0对x∈[-1,1]恒成立. ①设
,∵f(x)在[-1,1]上是增函数,∴f'(x)≥0对x∈[-1,1]恒成立,即x2-ax-2≤0对x∈[-1,1]恒成立. ①设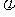 (x)=x2-ax-2,
(x)=x2-ax-2,
方法一:

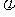 (1)=1-a-2≤0,
(1)=1-a-2≤0,
①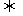
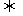 -1≤a≤1,∵对x∈[-1,1],f(x)是连续函数,且只有当a=1时,
-1≤a≤1,∵对x∈[-1,1],f(x)是连续函数,且只有当a=1时,
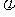 (-1)=1+a-2≤0.
(-1)=1+a-2≤0.
f'(-1)=0以及当a=-1时,f'(1)=0∴A={a|-1≤a≤1}.
方法二:
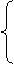
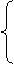
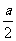 ≥0,
≥0,
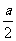 <0,
<0,
①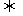 或
或
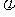 (-1)=1+a-2≤0
(-1)=1+a-2≤0 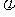 (1)=1-a-2≤0
(1)=1-a-2≤0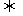 0≤a≤1或-1≤a≤0
0≤a≤1或-1≤a≤0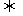 -1≤a≤1.
-1≤a≤1.
∵对x∈[-1,1],f(x)是连续函数,且只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0
∴A={a|-1≤a≤1}.
(Ⅱ)由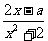 =
=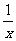 ,得x2-ax-2=0,∵△=a2+8>0∴x1,x2是方程x2-ax-2=0的两非零实根,
,得x2-ax-2=0,∵△=a2+8>0∴x1,x2是方程x2-ax-2=0的两非零实根,
 x1+x2=a,从而|x1-x2|=
x1+x2=a,从而|x1-x2|= =
=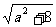 .∵-1≤a≤1,∴|x1-x2|=
.∵-1≤a≤1,∴|x1-x2|= ≤3
≤3
∴ 要使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,当且仅当m2+tm+1≥3对任意t∈[-1,1]恒成立,即m2+tm-2≥0对任意t∈[-1,1] 恒成立.
x1x2=-2,. ②设g(t)=m2+tm-2=mt+(m2-2),
方法一:
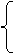 g(-1)=m2-m-2≥0,
g(-1)=m2-m-2≥0, m≥2或m≤-2. 所以,存在实数m,使不等式m2+tm+1≥|x1-x2|
m≥2或m≤-2. 所以,存在实数m,使不等式m2+tm+1≥|x1-x2|
②
g(1)=m2+m-2≥0,对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.
方法二:
当m=0时,②显然不成立;当m≠0时,
 m>0,
m<0,
m>0,
m<0, m≥2或m≤-2.
m≥2或m≤-2.
② g(-1)=m2-m-2≥0 或 g(1)=m2+m-2≥0
g(-1)=m2-m-2≥0 或 g(1)=m2+m-2≥0
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2
11(武清区2008~2009学年度期中22)

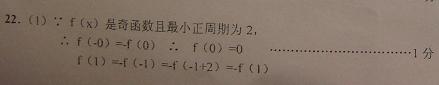


1(汉沽一中2009届月考文14).若实数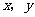 满足
满足 ,则
,则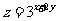 的最小值是
的最小值是
14 1
2(汉沽一中2008~2009届月考文13)、已知函数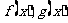 分别由下表给出:
分别由下表给出:
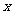 |
1 |
2 |
3 |
 |
1 |
3 |
1 |
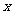 |
1 |
2 |
3 |
 |
3 |
2 |
1 |
则 的值 ;满足
的值 ;满足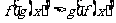 的
的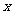 的值
.
的值
.
[答案]1,2
[命题意图]本题主要考查函数的值域、函数的大小比较以及考查学生的对表格的理解能力和分类讨论的数学思想方法.
[解析](1)∵ ,∴
,∴
(2)当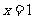 时,
时, ,∴
,∴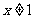 .
.
当 时,
时, ,∴
,∴ .
.
当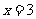 时,
时,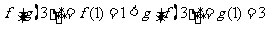 ,∴
,∴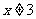 .
.
3(汉沽一中2009届月考文14).若实数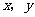 满足
满足 ,则
,则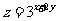 的最小值是
1
的最小值是
1
4(武清区2008~2009学年度第一学期期中质量调查试卷高三理)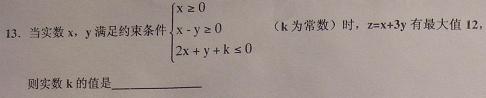

5(武清区2008~2009学年度期中理20)




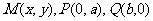
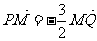 得
得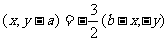 (2分)
(2分)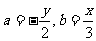 ,即
,即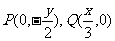 (4分)
(4分)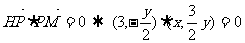
 (6分)
(6分) 消去
消去 得
得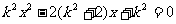
 (8分)
(8分)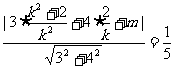

 ,
, ∴
∴  (11分)
(11分) ,则
,则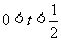

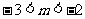 (14分)
(14分)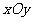 中,线段AB与y轴交于点
中,线段AB与y轴交于点 ,直线AB的斜率为K,且满足
,直线AB的斜率为K,且满足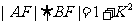 。
。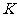 ,一定存在以y轴为对称轴且经过A、B、O三点的抛物线C,并求出抛物线C的方程;
,一定存在以y轴为对称轴且经过A、B、O三点的抛物线C,并求出抛物线C的方程; 与其交于M、N两点,求
与其交于M、N两点,求 和
和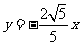 上的点,故可设
上的点,故可设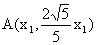 ,
, .
. ,
,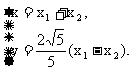 ∴
∴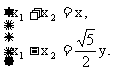 ………………………4分
………………………4分 ,
, .……………………………………5分
.……………………………………5分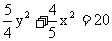 .
.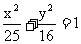 .………………………………………6分
.………………………………………6分 ,可得(x,y-16)=
,可得(x,y-16)=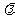 (s,t-16).
(s,t-16).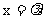 ,
,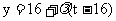 .……………………………………8分
.……………………………………8分 ……………………………………9分
……………………………………9分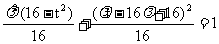 .
.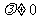 ,且
,且 ,
,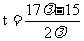 .………………………………………………………11分
.………………………………………………………11分 ,
∴
,
∴ .
. (
(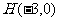 ,点P在y轴上,点Q在x轴正半轴上,点M在直线PQ上,且
,点P在y轴上,点Q在x轴正半轴上,点M在直线PQ上,且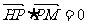
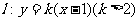 与轨迹C交于A、B两点,AB中点N到直线
与轨迹C交于A、B两点,AB中点N到直线
 的距离为
的距离为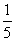 ,求m的取值范围。
,求m的取值范围。 ,它们在
,它们在 轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点。
轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点。 过点
过点 ,交抛物线于
,交抛物线于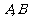 两点,是否存在垂直于
两点,是否存在垂直于 被以
被以 为直径的圆截得的弦长为定值?若存在,求出
为直径的圆截得的弦长为定值?若存在,求出 ,将
,将
 ………………………………………………(1分)
………………………………………………(1分)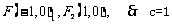 …………………(2分)
…………………(2分)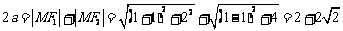
 ………………………………(4分)
………………………………(4分)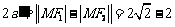
 ………………………………(6分)
………………………………(6分)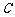 ,
, ,以
,以 两点,
两点, 中点为
中点为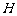
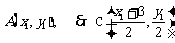 ………………………………………………(7分)
………………………………………………(7分)

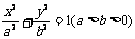 的焦点分别为
的焦点分别为 、
、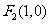 ,右准线
,右准线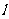 交
交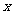 轴于点
轴于点 ,且
,且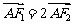 .
. (2)过
(2)过 、
、 分别作互相垂直的两直线与椭圆分别交于
分别作互相垂直的两直线与椭圆分别交于 、
、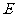 、
、 、
、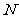 四点(如图所示),试求四边形
四点(如图所示),试求四边形 面积的最大值和最小值.
面积的最大值和最小值.

 为
为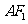 的中点
的中点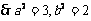 即:椭圆方程为
即:椭圆方程为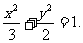
 与
与 ,此时
,此时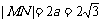 ,四边形
,四边形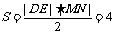 .同理当
.同理当 与
与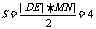 . 当直线
. 当直线 ,
, 均与
均与 :
: ,代入消去
,代入消去 设
设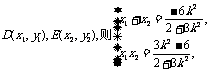 所以,
所以,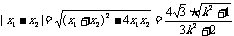 ,
所以,
,
所以,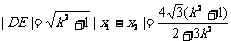 ,同理
,同理 所以四边形的面积
所以四边形的面积
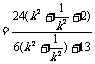 令
令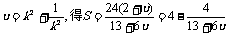 因为
因为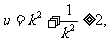 当
当 ,且S是以u为自变量的增函数,所以
,且S是以u为自变量的增函数,所以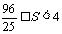 .
. 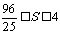 .故四边形
.故四边形 .
.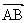 所成的比为λ,证明
所成的比为λ,证明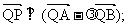
 (2)设直线AB的方程是x-2y+12=0,过A、B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
(2)设直线AB的方程是x-2y+12=0,过A、B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.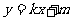 ,
,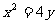 得:
得: …………… ①
…………………2分
…………… ①
…………………2分 所以
所以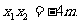
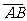 所成的比为
所成的比为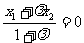 ,
即
,
即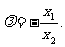 …………………4分
…………………4分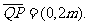
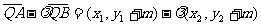
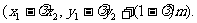
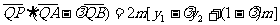

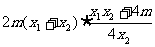
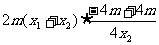
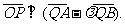 ………………………………………………………7分
………………………………………………………7分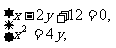 得点A、B的坐标分别是(6,9)、(--4,4).
得点A、B的坐标分别是(6,9)、(--4,4).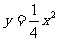 ,
,
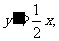
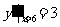 .…………………………9分
.…………………………9分 ,
,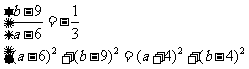 ……………………………11分
……………………………11分 …………………13分
…………………13分 .………………………………………………14分
.………………………………………………14分 上的两点,
上的两点,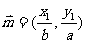 ,
,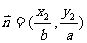 ,若
,若 且椭圆的离心率
且椭圆的离心率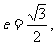
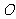 为坐标原点.
为坐标原点.
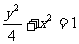 ……………………3分
……………………3分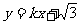
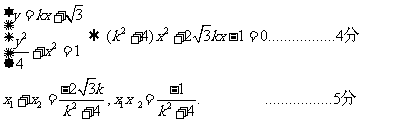
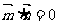 得:
得:
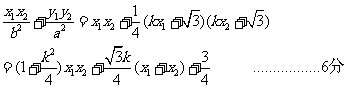
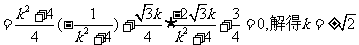 ……7分
……7分 ,由
,由 ……………………8分
……………………8分 在椭圆上,所以
在椭圆上,所以
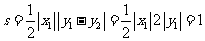
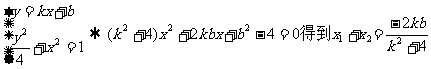
 ……………………10分
……………………10分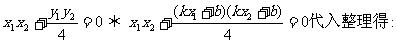
 ………………………………………12分
………………………………………12分
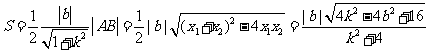

 ,
,
 是平面内一动点,直线
是平面内一动点,直线 、
、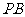 斜率之积为
斜率之积为 .
.  的方程;
的方程; 作直线
作直线 两点,线段
两点,线段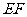 的中点为
的中点为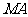 的斜率
的斜率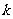 的取值范围.
的取值范围. ,依题意,有
,依题意,有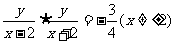 .
………………… 3分
.
………………… 3分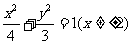 .
. , …………………………………………………………………………6分
, …………………………………………………………………………6分 消去
消去
 ,
, ,则
,则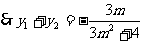 ,……………………………………………………… 8分
,……………………………………………………… 8分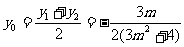
 ,
,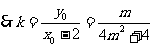 ,
…………………………………………… 10分
,
…………………………………………… 10分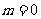 时,
时, ;
…………………………………………… 11分
;
…………………………………………… 11分 时,
时,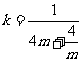
 .
. .
. 且
且 .
………………………………………… 13分
.
………………………………………… 13分 .……………… 14分
.……………… 14分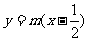 , …………7分
, …………7分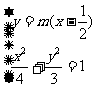 消去
消去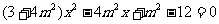
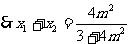 ,……………………………………………………… 8分
,……………………………………………………… 8分
 ,
,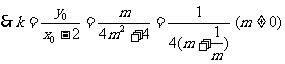 ,
………………… 10分
,
………………… 10分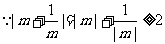
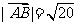 ,动点P满足
,动点P满足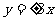 ,它的一个焦点是
,它的一个焦点是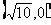 ,则双曲线的方程是__________.
,则双曲线的方程是__________. 
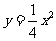 的焦点坐标是 (0,1)
的焦点坐标是 (0,1) 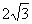

 的左、右焦点分别为
的左、右焦点分别为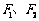 ,
,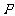 是准线上一点,且
是准线上一点,且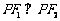 ,
,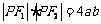 则双曲线的离心率是__ _。
则双曲线的离心率是__ _。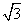
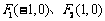 为焦点且与直线
为焦点且与直线 有公共点的椭圆中,离心率最大的椭圆方程是 ( C )
有公共点的椭圆中,离心率最大的椭圆方程是 ( C )
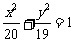 B.
B.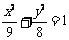 C.
C.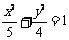 D.
D.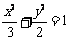
 (一中2008-2009月考理5).双曲线
(一中2008-2009月考理5).双曲线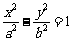 的右焦点为
的右焦点为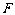 ,右准线与一条渐近线交于点
,右准线与一条渐近线交于点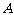 ,
,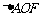 的面积为
的面积为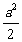 ,则两条渐近线的夹角为
( A )
,则两条渐近线的夹角为
( A )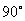 B.
B. C.
C.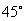 D.
D.
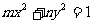 的一个焦点与抛物线
的一个焦点与抛物线 的焦点相同,离心率为2,则此双曲线的方程为 ( A )
的焦点相同,离心率为2,则此双曲线的方程为 ( A )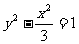 B.
B.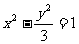 C.
C. D.
D.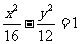
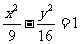 的右焦点为圆心,且与其渐近线相切的圆的方程是 (6.A )
的右焦点为圆心,且与其渐近线相切的圆的方程是 (6.A )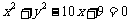 B.
B.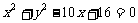
 D.
D.
 的焦点与椭圆
的焦点与椭圆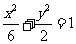 的右焦点重合,则
的右焦点重合,则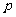 的值为(D )
的值为(D ) B.
B. C.
C. D.
D.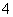

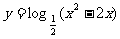 的定义域是
,单调递减区间是________________________. (-∞,0)∪(2,+∞), (2,+∞) (第一空3分,第二空2分)
的定义域是
,单调递减区间是________________________. (-∞,0)∪(2,+∞), (2,+∞) (第一空3分,第二空2分) ,则对于
,则对于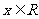 ,函数
,函数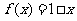 ,,则
,,则 12 1
12 1 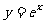 的切线,则切点的坐标为
,切线的斜率为 . (1,e), e (第一空3分,第二空2分)
的切线,则切点的坐标为
,切线的斜率为 . (1,e), e (第一空3分,第二空2分)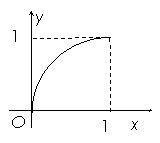 12.已知定义在区间
12.已知定义在区间 上的函数
上的函数 的任意
的任意 、
、 ,给出下列结论:
,给出下列结论: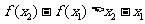 ;
; ;
;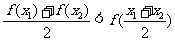 .
.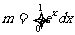 ,
, ,则
,则 的大小关系为__ _。
的大小关系为__ _。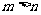
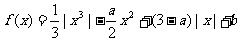 ,①若
,①若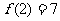 ,则
,则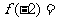 ;②若
;②若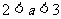
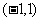 上的函数
上的函数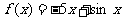 ,如果
,如果 ,则实数a的取值范围为 。
,则实数a的取值范围为 。
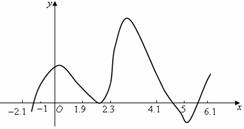 .下图是函数
.下图是函数 个不同的公共点.给出下列四个区间之中,存在不能用二分法求出的零点,该零点所在的区间是( 2.B )
个不同的公共点.给出下列四个区间之中,存在不能用二分法求出的零点,该零点所在的区间是( 2.B )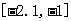 C.
C.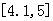
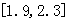 D.
D.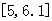
 (
汉沽一中2008~2009届月考理4).设
(
汉沽一中2008~2009届月考理4).设 时,
时,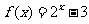 ,则
,则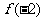 的值等于( C)
的值等于( C)  C.
C.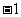 D.
D.
 ,其图象如图所示,则不等式
,其图象如图所示,则不等式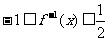 的解集为( C )
的解集为( C ) B.
B.
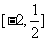
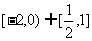 D.
D. 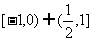

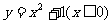 的图象关于直线
的图象关于直线 对称的图象的函数为
对称的图象的函数为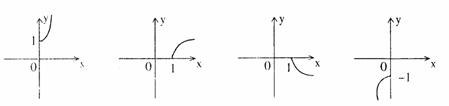
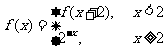 ,则
,则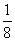 D.
D.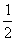
 (a>0,且a≠1)的图像过一个定点P,且点P在直线
(a>0,且a≠1)的图像过一个定点P,且点P在直线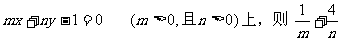 的最小值是 ( D )
的最小值是 ( D )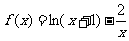 的零点所在的大致区间是(B)
的零点所在的大致区间是(B) B.
B.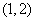 C.
C. D.
D.
 ,若
,若 ,则
,则 的取值范围是(D
)
A.
的取值范围是(D
)
A. B.
B. C.
C.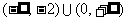 D.
D.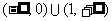
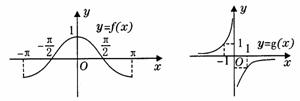
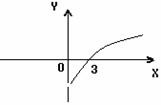 11(一中2008-2009月考理6).定义在
11(一中2008-2009月考理6).定义在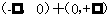 上的奇函数
上的奇函数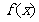 在
在 上为增函数,当
上为增函数,当 时,
时, 的图像如图所示,则不等式
的图像如图所示,则不等式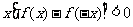 的解集是
( D )
的解集是
( D ) B.
B.
 D.
D.
 ,且当
,且当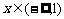 时,
时,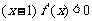 ,设
,设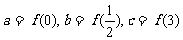 ,则
( B )
,则
( B )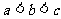 B.
B. C.
C.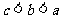 D.
D.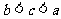
 ,若方程
,若方程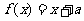 恰有两个不等的实根,则
恰有两个不等的实根,则 B.
B.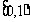 C.
C. D.
D.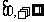

 (10.B )
(10.B )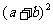 ,没有最小值
B.有最小值
,没有最小值
B.有最小值 D.没有最值
D.没有最值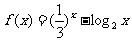 ,若实数
,若实数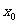 是方程
是方程 的解,且
的解,且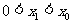 ,则
,则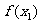 的值(C )
的值(C )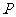 在平面区域
在平面区域 上,点
上,点 在曲线
在曲线 上,则
上,则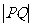 的最小值为
的最小值为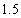 B.
B.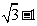 C.
C.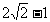 D.
D. ( A )
( A ) (2009年滨海新区五所重点学校联考理6).已知等比数列
(2009年滨海新区五所重点学校联考理6).已知等比数列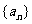 的各项均为正数,公比
的各项均为正数,公比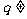 1,设
1,设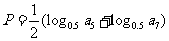 ,
, P与Q的大小关系是
( 6.D )
P与Q的大小关系是
( 6.D )  表示的平面区域的面积是9,那么实数
表示的平面区域的面积是9,那么实数 的值为 ( 7.D )
的值为 ( 7.D )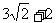 B.-
B.- ,则目标函数 z = x
+ 2 y 的取值范围是
( 3.A
)
,则目标函数 z = x
+ 2 y 的取值范围是
( 3.A
)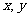 满足约束条件
满足约束条件 ,则目标函数
,则目标函数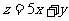 取得最大值时的点的坐标是
取得最大值时的点的坐标是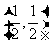 B.
B.  C.
C.  D.
D. 
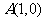 时
时 取得最大值,
取得最大值, .
.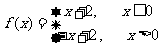 ,则不等式
,则不等式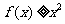 的解集是
的解集是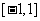 B.
B.
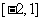 D.
D.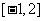
 .
.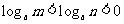 ,则A
,则A
 所表示的平面区域的面积为( D
)
所表示的平面区域的面积为( D
)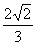 C.
C.
 D.
D. 