21.  的图象过点(-1,-6),且函数
的图象过点(-1,-6),且函数 的图象关于y轴对称.
的图象关于y轴对称.
(Ⅰ)求m、n的值及函数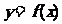 的单调区间;
的单调区间;
(Ⅱ)若a>0,求函数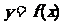 在区间(a -1,a+1)内的极值..
在区间(a -1,a+1)内的极值..
解:(Ⅰ)由函数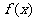 图象过点(-1,-6),得
图象过点(-1,-6),得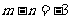 ,①
,①
由 ,得
,得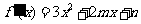 ,
,
则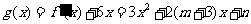 ;
;
而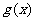 图象关于y轴对称,
图象关于y轴对称,
所以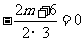 ,所以
,所以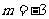 , 代入①得
, 代入①得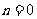 .
.
于是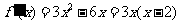 .
.
由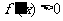 得
得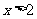 或
或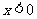 ,
,
故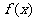 的单调递增区间是(-∞,0),(2,+∞);
的单调递增区间是(-∞,0),(2,+∞);
由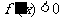 得
得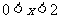 ,
,
故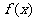 的单调递减区间是(0,2).
的单调递减区间是(0,2).
(Ⅱ)由(Ⅰ)得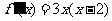 ,
,
令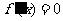 得
得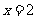 或
或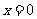 .
.
当x变化时,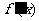 、
、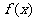 的变化情况如下表:
的变化情况如下表:
|
x |
(-∞.0) |
0 |
(0,2) |
2 |
(2,+ ∞) |
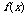 |
+ |
0 |
- |
0 |
+ |
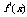 |
↗ |
极大值 |
↘ |
极小值 |
↗ |
由此可得:
当0<a<1时,f(x)在(a-1,a+1)内有极大值f(O)=-2,无极小值;
当a=1时,f(x)在(a-1,a+1)内无极值;
当1<a<3时,f(x)在(a-1,a+1)内有极小值f(2)=-6,无极大值;
当a≥3时,f(x)在(a-1,a+1)内无极值.
综上得:
当0<a<1时,f(x)有极大值-2,无极小值,
当1<a<3时,f(x)有极小值-6,无极大值;
当a=1或a≥3时,f(x)无极值.
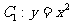 相切于点
相切于点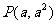 ,又与抛物线
,又与抛物线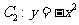 相交于两点A、B. 分别过A、B作
相交于两点A、B. 分别过A、B作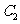 的切线
的切线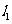 ,
,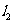 相交于点Q,设
相交于点Q,设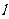 ,
,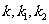 .
.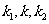 成等差数列;
成等差数列;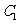 上.
上.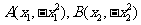 ,
,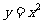 求导得
求导得 ;
;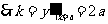 ,
,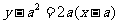 ,即
,即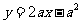 ,代入
,代入 得
得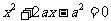 ,
,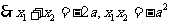 .
. ;
;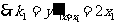 ,
, ;
;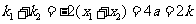 ,
,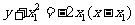 ,即
,即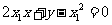 ,
,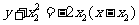 ,即
,即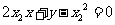 ,
,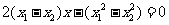 ,
,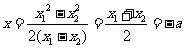 ,
,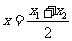 代入
代入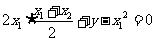 ,
,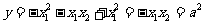 ,
,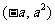 ,显然满足
,显然满足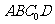 中,
中,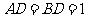 ,
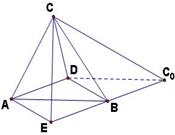
,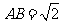 .沿它的对角线
.沿它的对角线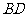 把
把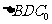 折起,使点
折起,使点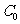 到达平面
到达平面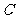 的位置.
的位置.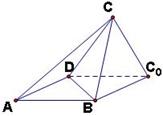 (Ⅰ)证明:平面
(Ⅰ)证明:平面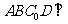 平面
平面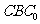 ;
;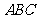 为等腰三角形,求二面角
为等腰三角形,求二面角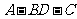 的大小。
的大小。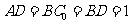 ,
,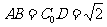 ,所以
,所以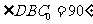 .
.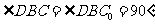 ,
,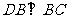 ,又
,又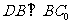 ,故
,故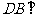 平面
平面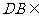 平面
平面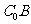 到
到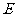 ,使
,使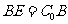 ,连结
,连结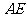 ,
,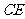 。
。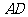

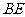 ,
,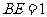 ,
,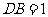 ,
,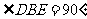 ,所以
,所以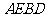 为正方形,
为正方形,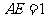 。
。 由于
由于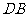 都与平面
都与平面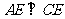 ,可知
,可知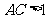 。
。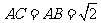 时,△
时,△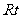 △
△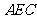 中,
中,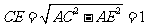 ,又
,又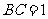 ,
,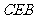 为等边三角形,
为等边三角形,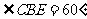 。
。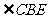 为二面角
为二面角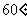 。
。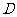 为坐标原点,射线
为坐标原点,射线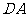 ,
,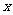 轴正半轴和
轴正半轴和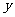 轴正半轴,建立如图的空间直角坐标系
轴正半轴,建立如图的空间直角坐标系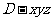 ,则
,则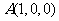 ,
,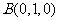 ,
,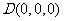 。
。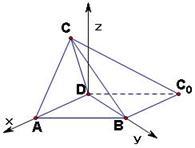 由(Ⅰ)可设点
由(Ⅰ)可设点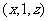 ,其中
,其中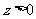 ,则有
,则有 。 ①
。 ①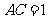 或
或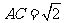 。
。 。
。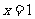 ,
,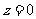 ,不合题意。
,不合题意。 。
②
。
②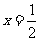 ,
,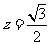 。故点
。故点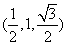 。
。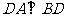 ,
,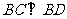 ,所以
,所以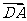 与
与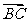 夹角的大小等于二面角
夹角的大小等于二面角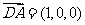 ,
,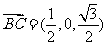 ,
,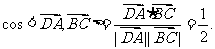
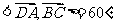 即二面角
即二面角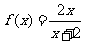 ,定义数列
,定义数列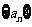 ,使:
,使: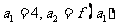 ,…,
,…,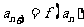 … .
… . 是等差数列;
是等差数列; 的前n项和为
的前n项和为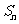 ,求
,求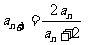
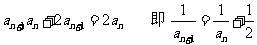
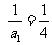 ∴数列{
∴数列{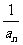 }是以
}是以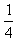 为首项,以
为首项,以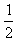 为公差的等差数列.
为公差的等差数列.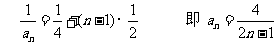
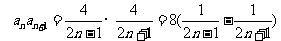
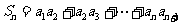
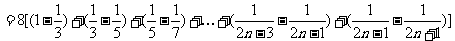
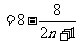 .
.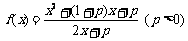
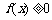 ;
;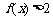 对
对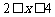 时恒成立,求p的范围..
时恒成立,求p的范围..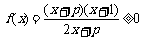
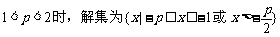
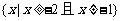
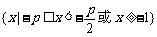
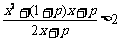
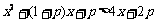
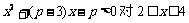 恒成立
恒成立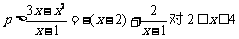 恒成立
恒成立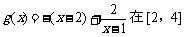 上递减
上递减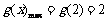
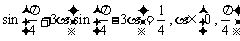 ,求
,求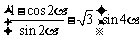 的值.
的值.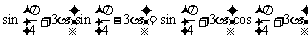
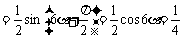 ,
,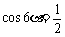 ,又∵
,又∵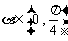 ,∴
,∴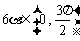
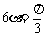 ,即
,即 .
.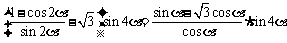
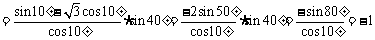
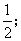
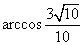 ;
;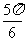 .
.