摘要:17.已知.求的值. 解: . 即.又∵.∴ ∴.即. ∴
网址:http://m.1010jiajiao.com/timu_id_3993562[举报]
已知点列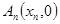 满足:
满足: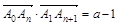 ,其中
,其中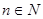 ,又已知
,又已知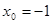 ,
,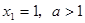 .
.
(I)若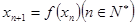 ,求
,求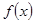 的表达式;
的表达式;
(II)已知点B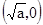 ,记
,记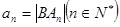 ,且
,且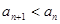 成立,试求a的取值范围;
成立,试求a的取值范围;
(III)设(2)中的数列 的前n项和为
的前n项和为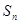 ,试求:
,试求: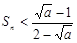 。
。
【解析】第一问利用∵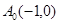 ,
,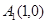 ,∴
,∴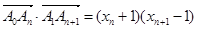 ∴
∴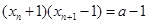 ,∴
,∴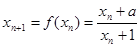 ,∴
,∴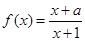
第二问∵ ,∴
,∴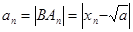 .
.
∵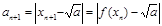
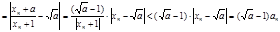
∴要使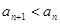 成立,只要
成立,只要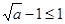 ,即
,即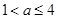 ∴
∴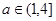 为所求
为所求
第三问∵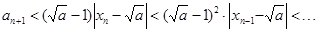
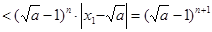 ,∴
,∴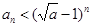
∴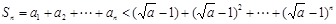
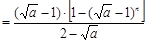 ∵
∵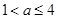 ,∴
,∴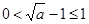 ,∴
,∴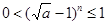 ∴
∴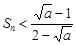
查看习题详情和答案>>
仔细阅读下面问题的解法:
设A=[0,1],若不等式21-x-a>0在A上有解,求实数a的取值范围.
解:由已知可得 a<21-x
令f(x)=21-x,不等式a<21-x在A上有解,
∴a<f(x)在A上的最大值
又f(x)在[0,1]上单调递减,f(x)max=f(0)=2
∴a<2即为所求.
学习以上问题的解法,解决下面的问题:
(1)已知函数f(x)=x2+2x+3 (-2≤x≤-1)求f(x)的反函数及反函数的定义域A;
(2)对于(1)中的A,设g(x)=
x∈A,试判断g(x)的单调性;(不证)
(3)又若B={x|
>2x+a-5},若A∩B≠Φ,求实数a的取值范围.
查看习题详情和答案>>
设A=[0,1],若不等式21-x-a>0在A上有解,求实数a的取值范围.
解:由已知可得 a<21-x
令f(x)=21-x,不等式a<21-x在A上有解,
∴a<f(x)在A上的最大值
又f(x)在[0,1]上单调递减,f(x)max=f(0)=2
∴a<2即为所求.
学习以上问题的解法,解决下面的问题:
(1)已知函数f(x)=x2+2x+3 (-2≤x≤-1)求f(x)的反函数及反函数的定义域A;
(2)对于(1)中的A,设g(x)=
| 10-x |
| 10+x |
(3)又若B={x|
| 10-x |
| 10+x |
仔细阅读下面问题的解法:
设A=[0,1],若不等式21-x-a>0在A上有解,求实数a的取值范围.
解:由已知可得 a<21-x
令f(x)=21-x,不等式a<21-x在A上有解,
∴a<f(x)在A上的最大值
又f(x)在[0,1]上单调递减,f(x)max=f(0)=2
∴a<2即为所求.
学习以上问题的解法,解决下面的问题:
(1)已知函数f(x)=x2+2x+3 (-2≤x≤-1)求f(x)的反函数及反函数的定义域A;
(2)对于(1)中的A,设g(x)= x∈A,试判断g(x)的单调性;(不证)
x∈A,试判断g(x)的单调性;(不证)
(3)又若B={x| >2x+a-5},若A∩B≠Φ,求实数a的取值范围.
>2x+a-5},若A∩B≠Φ,求实数a的取值范围.
查看习题详情和答案>>
仔细阅读下面问题的解法:
设A=[0,1],若不等式21-x-a>0在A上有解,求实数a的取值范围.
由已知可得 a<21-x
令f(x)=21-x,不等式a<21-x在A上有解,
∴a<f(x)在A上的最大值
又f(x)在[0,1]上单调递减,f(x)max=f(0)=2
∴a<2即为所求.
学习以上问题的解法,解决下面的问题:
(1)已知函数f(x)=x2+2x+3 (-2≤x≤-1)求f(x)的反函数及反函数的定义域A;
(2)对于(1)中的A,设g(x)=
x∈A,试判断g(x)的单调性;(不证)
(3)又若B={x|
>2x+a-5},若A∩B≠Φ,求实数a的取值范围.
查看习题详情和答案>>
设A=[0,1],若不等式21-x-a>0在A上有解,求实数a的取值范围.
由已知可得 a<21-x
令f(x)=21-x,不等式a<21-x在A上有解,
∴a<f(x)在A上的最大值
又f(x)在[0,1]上单调递减,f(x)max=f(0)=2
∴a<2即为所求.
学习以上问题的解法,解决下面的问题:
(1)已知函数f(x)=x2+2x+3 (-2≤x≤-1)求f(x)的反函数及反函数的定义域A;
(2)对于(1)中的A,设g(x)=
| 10-x |
| 10+x |
(3)又若B={x|
| 10-x |
| 10+x |