摘要： 已知函数.定义数列.使:.-.- ． (1)求证:数列是等差数列, (2)设数列的前n项和为.求． 解:(1)∵ ∴ ∴ 又 ∴数列{}是以为首项.以为公差的等差数列． 可知 ∴ ∴ . 19:已知 (1)若p > 1时.解关于x的不等式, (2)若对时恒成立.求p的范围．． 解:(1) ① ② p = 2时.解集为 ③ p > 2时.解集为 (2) ∴ 恒成立 ∴ 恒成立 ∵ 上递减 ∴ ∴ p > 2．
网址：http://m.1010jiajiao.com/timu_id_3993563[举报]
，是否存在实数a、b、c，使
同时满足下列三个条件：（1）定义域为R的奇函数；（2）在
上是增函数；（3）最大值是1．若存在，求出a、b、c；若不存在，说明理由．
，是否存在实数a、b、c，使
同时满足下列三个条件：（1）定义域为R的奇函数；（2）在
上是增函数；（3）最大值是1．若存在，求出a、b、c；若不存在，说明理由．
，是否存在实数a、b、c，使
同时满足下列三个条件：（1）定义域为R的奇函数；（2）在
上是增函数；（3）最大值是1．若存在，求出a、b、c；若不存在，说明理由.
，是否存在实数a、b、c，使
同时满足下列三个条件：（1）定义域为R的奇函数；（2）在
上是增函数；（3）最大值是1．若存在，求出a、b、c；若不存在，说明理由.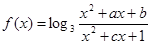
，是否存在实数a、b、c，使
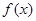同时满足下列三个条件：（1）定义域为R的奇函数；（2）在
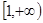上是增函数；（3）最大值是1．若存在，求出a、b、c；若不存在，说明理由.