1.例题:
例1.下表给出了我国从 年至
年至 年人口数据资料,试根据表中数据估计我国
年人口数据资料,试根据表中数据估计我国 年的人口数.
年的人口数.
|
年份 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
人口数/百万 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
解:为了简化数据,先将年份减去 ,并将所得值用
,并将所得值用 表示,对应人口数用
表示,对应人口数用 表示,得到下面的数据表:
表示,得到下面的数据表:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 [来源:] [来源:] |
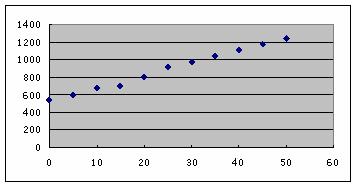 作出
作出 个点
个点 构成的散点图,
构成的散点图,
由图可知,这些点在一条直线附近,可以用线性回归模型 来表示它们之间的关系.
来表示它们之间的关系.
根据公式(1)可得

这里的 分别为
分别为 的估
的估
计值,因此线性回归方程
为
由于 年对应的
年对应的 ,代入线性回归方程
,代入线性回归方程 可得
可得 (百万),即
(百万),即 年的人口总数估计为13.23亿.
年的人口总数估计为13.23亿.
例2. 某地区对本地的企业进行了一次抽样调查,下表是这次抽查中所得到的各企业的人均资本 (万元)与人均产出
(万元)与人均产出 (万元)的数据:
(万元)的数据:
|
人均 资本  /万元 /万元 |
 |
 |
  |
 |
 |
 |
 |
 |
 |
 |
|
人均 产出  /万元 /万元 |
 |
 |
 |
 |
  |
 |
 |
 |
 |
 |
(1)设 与
与 之间具有近似关系
之间具有近似关系 (
( 为常数),试根据表中数据估计
为常数),试根据表中数据估计 和
和 的值;
的值;
(2)估计企业人均资本为 万元时的人均产出(精确到
万元时的人均产出(精确到 ).
).
分析:根据 ,
, 所具有的关系可知,此问题不是线性回归问题,不能直接用线性回归方程处理.但由对数运算的性质可知,只要对
所具有的关系可知,此问题不是线性回归问题,不能直接用线性回归方程处理.但由对数运算的性质可知,只要对 的两边取对数,就能将其转化为线性关系.
的两边取对数,就能将其转化为线性关系.
解(1)在 的两边取常用对数,可得
的两边取常用对数,可得 ,设
,设 ,
, ,
, ,则
,则 .相关数据计算如图
.相关数据计算如图 所示.
所示.
|
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
1 |
人均资本 /万元 /万元 |
3 |
4 |
5.5 |
6.5 |
7 |
8 |
9 |
10.5 |
11.5 |
14 |
|
2 |
人均产出 /万元 /万元 |
4.12 |
4.67 |
8.68 |
11.01 |
13.04 |
14.43 |
17.5 |
25.46 |
26.66 |
45.2 |
|
3 |
 |
0.47712 |
0.60 206 206 |
0.74036 |
0.81291 |
0. 8451 8451 |
0.90309 |
0.95424 |
1.02119 |
1.0607 |
1.14613 |
|
4 |
 |
0.6149 |
0.66932 |
0.93852 |
1.04179 |
1.11528 |
1.15927 |
1.24304 |
1.40586 |
1.42586 |
1.65514 |
仿照问题情境可得 ,
, 的估计值
的估计值 ,
, 分
分 别为
别为 由
由 可得
可得 ,即
,即 ,
, 的估计值分别为
的估计值分别为 和
和 .
.
(2)由(1)知 .样本数据及回归曲线的图形如图
.样本数据及回归曲线的图形如图 (见书本
(见书本 页)
页)
当 时,
时, (万元),故当企业人均资本为
(万元),故当企业人均资本为 万元时,人均产值约为
万元时,人均产值约为 万元.
万元.
 中
中 相比,它表示
相比,它表示 题.
题. ,令
,令 ,
, ,则有
,则有 .
. ,
, ,则有
,则有 .
. ,令
,令 ,令
,令 ,令
,令