19．已知$\overrightarrow a=(1.1)$.$\overrightarrow b=(1.0)$.则$|{\overrightarrow a-2\overrightarrow b}|$——青夏教育精英家教网——

19．已知$\overrightarrow a=（1，1）$，$\overrightarrow b=（1，0）$，则$|{\overrightarrow a-2\overrightarrow b}|$=$\sqrt{2}$．

18．已知函数$f（x）=2lnx（\frac{1}{e}≤x≤{e^2}）$，g（x）=mx+2，若f（x）与g（x）的图象上存在关于直线y=1对称的点，则实数m的取值范围是（　　）

$[-\frac{2}{3}，-\frac{4}{e^2}]$

$[-\frac{2}{e}，2e]$

$[-\frac{4}{e^2}，2e]$

$[-\frac{4}{e^2}，+∞]$

如图，一直角墙角，两边的长度足够长，若P处有一棵树与两墙的距离分别是2m和αm（0＜α＜10），不考虑树的粗细，现用12m长的篱笆，借助墙角围成一个矩形花圃ABCD，设此矩形花圃的最大面积为u，若将这棵树围在矩形花圃内，则函数u=f（a）（单位：m²）的图象大致是（　　）

	A．			B．
	C．			D．

16．设F是双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）的左焦点，M在双曲线的右支上，且MF的中点恰为该双曲线的虚轴的一个端点，则C的渐近线方程为（　　）

$y=±\frac{1}{2}x$

$y=±\frac{{\sqrt{5}}}{5}x$

$y=±\sqrt{5}x$

15．若圆C与y轴相切于点P（0，1），与x轴的正半轴交于A，B两点，且|AB|=2，则圆C的标准方程是（　　）

${（x+\sqrt{2}）^2}+{（y+1）^2}=2$

${（x+1）^2}+{（y+\sqrt{2}）^2}=2$

${（x-\sqrt{2}）^2}+{（y-1）^2}=2$

${（x-1）^2}+{（y-\sqrt{2}）^2}=2$

14．已知数列{a_n}是递增的等比数列，a₁+a₃+a₅=21，a₃=6，则a₅+a₇+a₉=（　　）

13．若x是实数，i是虚数单位，且（1+xi）（x-i）=-i，则x=（　　）

12．已知集合A={x|x²-4x≤0，x∈Z}，B={y|y=m²，m∈A}，则A∩B=（　　）

11．已知椭圆C：4x²+y²=4m²（m＞0），过原点的直线与椭圆C交于A，B两点，点P是椭圆上的任意一点且直线PA，PB与坐标轴不平行．
（1）证明：直线PA的斜率与直线PB斜率之积为定值；
（2）若A，B不是椭圆C的顶点，且PA⊥AB，直线BP与x轴，y轴分别交于E，F两点．
（i）证明：直线BP的斜率与直线AF斜率之比为定值；
（ii）记△OEF的面积为S_△OEF，求$\frac{{{S_{△OEF}}}}{m^2}$的最大值．

某市在对高三学生的4月理科数学调研测试的数据统计显示，全市10000名学生的成绩服从正态分布X～N（110，144），现从甲校100分以上的200份试卷中用系统抽样的方法抽取了20份试卷来分析，统计如下：

试卷编号	n₁	n₂	n₃	n₄	n₅	n₆	n₇	n₈	n₉	n₁₀
试卷得分	109	118	112	114	126	128	127	124	126	120
试卷编号	n₁₁	n₁₂	n₁₃	n₁₄	n₁₅	n₁₆	n₁₇	n₁₈	n₁₉	n₂₀
试卷得分	135	138	135	137	135	139	142	144	148	150

（注：表中试卷编号n₁＜n₂＜28＜n₄＜n₅＜…＜n₂₀）

（1）列出表中试卷得分为126分的试卷编号（写出具体数据）；
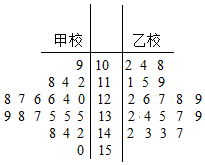
（2）该市又从乙校中也用系统抽样的方法抽取了20份试卷，将甲乙两校这40份试卷的得分制作了茎叶图（如图），试通过茎叶图比较两校学生成绩的平均分及分散程度（均不要求计算出具体值，给出结论即可）；
（3）在第（2）问的前提下，从甲乙两校这40名学生中，从成绩在140分以上（含140分）的学生中任意抽取3人，该3人在全市前15名的人数记为ξ，求ξ的分布列和期望．
（附：若随机变量X服从正态分布N（μ，σ²），则P（μ-σ＜X＜μ+σ）=68.3%，P（μ-2σ＜X＜μ+2σ）=95.4%，P（μ-3σ＜X＜μ+3σ）=99.7%）

0 240414 240422 240428 240432 240438 240440 240444 240450 240452 240458 240464 240468 240470 240474 240480 240482 240488 240492 240494 240498 240500 240504 240506 240508 240509 240510 240512 240513 240514 240516 240518 240522 240524 240528 240530 240534 240540 240542 240548 240552 240554 240558 240564 240570 240572 240578 240582 240584 240590 240594 240600 240608 266669