题目内容
11.已知椭圆C:4x2+y2=4m2(m>0),过原点的直线与椭圆C交于A,B两点,点P是椭圆上的任意一点且直线PA,PB与坐标轴不平行.(1)证明:直线PA的斜率与直线PB斜率之积为定值;
(2)若A,B不是椭圆C的顶点,且PA⊥AB,直线BP与x轴,y轴分别交于E,F两点.
(i)证明:直线BP的斜率与直线AF斜率之比为定值;
(ii)记△OEF的面积为S△OEF,求$\frac{{{S_{△OEF}}}}{m^2}$的最大值.
分析 (1)设A(x1,y1),P(x2,y2),则B(-x1,-y1),把A,P坐标代入椭圆方程,写出PA,PB的斜率,化简整理可得直线PA的斜率与直线PB斜率之积为定值;
(2)(i)由(1)得${k_{AB}}=\frac{y_1}{x_1}$,再由PA⊥AB,求得PA的斜率,进一步得到PB的斜率,写出PB所在直线方程,求得E,F的坐标,即可得到直线BP的斜率与直线AF斜率之比为定值;
(ii)由三角形面积公式写出△OEF的面积,由基本不等式可得其最大值,除以m2得答案.
解答 (1)证明:设A(x1,y1),P(x2,y2),则B(-x1,-y1),
∴$4{{x}_{1}}^{2}+{{y}_{1}}^{2}=4{m}^{2}$,$4{{x}_{2}}^{2}+{{y}_{2}}^{2}=4{m}^{2}$,
∴${k}_{PA}•{k}_{PB}=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}•\frac{{y}_{2}+{y}_{1}}{{x}_{2}+{x}_{1}}=\frac{{{y}_{2}}^{2}-{{y}_{1}}^{2}}{{{x}_{2}}^{2}-{{x}_{1}}^{2}}$=$\frac{(4{m}^{2}-4{{x}_{2}}^{2})-(4{m}^{2}-4{{x}_{1}}^{2})}{{{x}_{2}}^{2}-{{x}_{1}}^{2}}$=-4;
(2)证明:(i)由(1)得${k_{AB}}=\frac{y_1}{x_1}$,
又∵PA⊥AB,∴kAB•kPA=-1,得${k_{PA}}=-\frac{x_1}{y_1}$,
∵kPA•kPB=-4,∴${k_{PB}}=\frac{{4{y_1}}}{x_1}$.
∴直线BP:$y=\frac{{4{y_1}}}{x_1}(x+{x_1})-{y_1}$,则$E({-\frac{3}{4}{x_1},\;\;0})$,F(0,3y1),
则${k_{AF}}=\frac{{{y_1}-3{y_1}}}{{{x_1}-0}}=-2\frac{y_1}{x_1}$,
∴$\frac{{k}_{PB}}{{k}_{AF}}=\frac{4{y}_{1}}{{x}_{1}}•\frac{-2{y}_{1}}{{x}_{1}}=-2$.
(ii)解:∵${S_{△OEF}}=\frac{1}{2}|{({-\frac{3}{4}{x_1}})•3{y_1}}|=\frac{9}{8}|{x_1}•{y_1}|=\frac{9}{16}|2{x_1}•{y_1}|≤\frac{9}{16}•\frac{4x_1^2+y_1^2}{2}=\frac{9}{8}{m^2}$,
∴$\frac{{{S_{△OEF}}}}{m^2}≤\frac{9}{8}$,
当且仅当$x_1^2=\frac{m^2}{2},\;\;y_1^2=2{m^2}$时取到最大值.
即$\frac{{{S_{△OEF}}}}{m^2}$的最大值为$\frac{9}{8}$.
点评 本题考查椭圆的简单性质,考查直线与椭圆位置关系的应用,训练了利用基本不等式求最值,是中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{2\sqrt{5}}{3}$ | B. | 2 | C. | $\frac{5\sqrt{5}}{3}$ | D. | $\sqrt{5}$ |
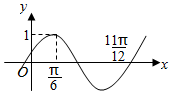 函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的图象如图所示,将f(x)的图象向右平移m个单位得到g(x)的图象关于y轴对称,则正数m的最小值为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的图象如图所示,将f(x)的图象向右平移m个单位得到g(x)的图象关于y轴对称,则正数m的最小值为( )| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
| A. | $y=±\frac{1}{2}x$ | B. | y=±2x | C. | $y=±\frac{{\sqrt{5}}}{5}x$ | D. | $y=±\sqrt{5}x$ |
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
 已知四棱台ABCD-A1B1C1D1的下底面是边长为4的正方形,AA1=4,且AA1⊥面ABCD,点P为DD1的中点,点Q在BC上,BQ=3QC,DD1与面ABCD所成角的正切值为2.
已知四棱台ABCD-A1B1C1D1的下底面是边长为4的正方形,AA1=4,且AA1⊥面ABCD,点P为DD1的中点,点Q在BC上,BQ=3QC,DD1与面ABCD所成角的正切值为2.