13．已知正六棱锥S-ABCDEF的底面边长和高均为1.则异面直线SC与DE所成角的大小为450．．——青夏教育精英家教网——

13．已知正六棱锥S-ABCDEF的底面边长和高均为1，则异面直线SC与DE所成角的大小为45⁰．．

12．一口袋中装有大小相同的2个白球和4个黑球，每次从袋中任意摸出一个球，若采取不放回抽样方式，从中摸出两个球，则摸得白球的个数X的方差D（X）=$\frac{16}{45}$．

11．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右焦点分别为F₁，F₂，P为双曲线右支上一点（异于右顶点），△PF₁F₂的内切圆与x轴切于点（2，0），过F₂作直线l与双曲线交于A，B两点，若使|AB|=b²的直线l恰有三条，则双曲线离心率的取值范围是（　　）

（1，$\sqrt{2}$）

（$\sqrt{2}$，+∞）

10．双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的半焦距为c，顶点A（a，0）到渐近线的距离为$\frac{\sqrt{2}}{3}$c，则双曲线的离心率为$\frac{\sqrt{6}}{2}$．

9．在平面直角坐标系式xOy中，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F₁（-c，0）、F₂（c，0），已知（1，e）和（e，$\frac{\sqrt{3}}{2}$）都在椭圆上，其中e为椭圆的离心率．
（1）求椭圆C的方程；
（2）过点F₂的直线l与椭圆C相交于P，Q两点，且$\overrightarrow{P{F}_{2}}$•$\overrightarrow{{F}_{1}Q}$+$\overrightarrow{{F}_{1}{F}_{2}}$•$\overrightarrow{Q{F}_{2}}$=4，求直线l的方程．

8．已知集合A={x|$\frac{x-1}{x+2}$≤0}，B={x|x＜-2}，则A∪（∁_UB）=（　　）

（-2，+∞）

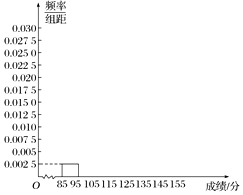高三年级有500名学生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在一次测试中的数学成绩，制成如下频率分布表：

分组	频数	频率
[85，95）	①	②
[95，105）		0.050
[105，115）		0.200
[115，125）	12	0.300
[125，135）		0.275
[135，145）	4	③
[145，155]		0.050
合计		④

（1）表格中①②③④处的数值分别为1、0.025、0.100、1.000；
（2）在图中画出[85，155]的频率分布直方图；
（3）根据题干信息估计总体平均数，并估计总体落在[125，155]上的频率．

6．已知A（3，5，2），B（-1，2，1），把$\overrightarrow{AB}$按向量$\overrightarrow{a}$=（2，1，1）平移后所得的向量是（　　）

（-4，-3，-1）

（-4，-3，0）

（-2，-1，0）

（-2，-2，0）

5．斜率为$\frac{1}{2}$且过点（2，2）的直线交抛物线y²=4x于A，B两点，求|AB|．

4．如图，某港口一天的水深变化曲线近似满足函数y=Asin$\frac{π}{6}$t+k，则水深从最小值变化到最大值至少需要（　　）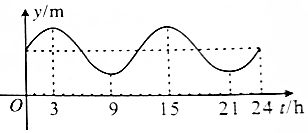

0 239947 239955 239961 239965 239971 239973 239977 239983 239985 239991 239997 240001 240003 240007 240013 240015 240021 240025 240027 240031 240033 240037 240039 240041 240042 240043 240045 240046 240047 240049 240051 240055 240057 240061 240063 240067 240073 240075 240081 240085 240087 240091 240097 240103 240105 240111 240115 240117 240123 240127 240133 240141 266669