题目内容
7. 高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:| 分组 | 频数 | 频率 |
| [85,95) | ① | ② |
| [95,105) | 0.050 | |
| [105,115) | 0.200 | |
| [115,125) | 12 | 0.300 |
| [125,135) | 0.275 | |
| [135,145) | 4 | ③ |
| [145,155] | 0.050 | |
| 合计 | ④ |
(2)在图中画出[85,155]的频率分布直方图;
(3)根据题干信息估计总体平均数,并估计总体落在[125,155]上的频率.
分析 (1)根据[115,125)内的频数和频率求出样本容量,
再计算表格中①②③④处的数值;
(2)在图中画出[85,155]的频率分布直方图即可;
(3)根据频率分布直方图,计算平均数以及[125,155]上的频率值.
解答 解:(1)根据频率表知,[115,125)内的频数为12,频率为0.300,
∴样本容量为$\frac{12}{0.300}$=40;
由频率分布直方图知,[85,95)内的频率为0.0025×10=0.025,
频数为40×0.025=1,∴表格中①处数值是1,②处数值是0.025;
根据频率和为1,知③处数值是1-0.025-0.050-0.200-0.300-0.275-0.050=0.100;
④处的数值是1.000;
故表格中①②③④处的数值分别为:1、0.025、0.100、1.000;
(2)在图中画出[85,155]的频率分布直方图,如图所示;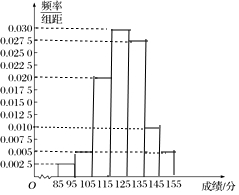
(3)根据频率分布直方图,计算平均数为
$\overline{x}$=90×0.025+100×0.05+110×0.2+120×0.3+130×0.275+140×0.1+150×0.05=122.5,
即估计总体平均数为122.5;
估计总体在[125,155]上的频率为0.275+0.100+0.050=0.425.
点评 本题考查了频率分布直方图的应用问题,也考查了识图、用图的能力,是中档题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
4.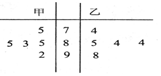 如图是某班甲、乙两位同学在5次阶段性检测中的数学成绩(百分制)的茎叶图,甲、乙两位同学得分的中位数分别为x1,x2,得分的方差分别为y1,y2,则下列结论正确的是( )
如图是某班甲、乙两位同学在5次阶段性检测中的数学成绩(百分制)的茎叶图,甲、乙两位同学得分的中位数分别为x1,x2,得分的方差分别为y1,y2,则下列结论正确的是( )
 如图是某班甲、乙两位同学在5次阶段性检测中的数学成绩(百分制)的茎叶图,甲、乙两位同学得分的中位数分别为x1,x2,得分的方差分别为y1,y2,则下列结论正确的是( )
如图是某班甲、乙两位同学在5次阶段性检测中的数学成绩(百分制)的茎叶图,甲、乙两位同学得分的中位数分别为x1,x2,得分的方差分别为y1,y2,则下列结论正确的是( )| A. | x1<x2,y1<y2 | B. | x1<x2,y1>y2 | C. | x1>x2,y1>y2 | D. | x1>x2,y1<y2 |
19.已知函数f(x)=lnx+x2+x.正实数x1,x2满足f(x1)+f(x2)+x1x2=0,则下述结论中正确的一项是( )
| A. | x1+x2≥$\frac{\sqrt{5}-1}{2}$ | B. | x1+x2<$\frac{\sqrt{5}-1}{2}$ | C. | x1+x2≥$\frac{\sqrt{5}+1}{2}$ | D. | x1+x2<$\frac{\sqrt{5}+1}{2}$ |