题目内容
12.一口袋中装有大小相同的2个白球和4个黑球,每次从袋中任意摸出一个球,若采取不放回抽样方式,从中摸出两个球,则摸得白球的个数X的方差D(X)=$\frac{16}{45}$.分析 根据题意知随机变量X的可能取值,计算对应的概率值,求出数学期望和方差.
解答 解:根据题意,摸得白球的个数为X,则X的可能取值为0,1,2;
计算P(X=0)=$\frac{4}{6}$×$\frac{3}{5}$=$\frac{2}{5}$,
p(X=1)=$\frac{4}{6}$×$\frac{2}{5}$+$\frac{2}{6}$×$\frac{4}{5}$=$\frac{8}{15}$,
p(X=2)=$\frac{2}{6}$×$\frac{1}{5}$=$\frac{1}{15}$;
∴随机变量X的数学期望为:
E(X)=0×$\frac{2}{5}$+1×$\frac{8}{15}$+2×$\frac{1}{15}$=$\frac{2}{3}$,
方差为:D(X)=${(0-\frac{2}{3})}^{2}$×$\frac{2}{5}$+${(1-\frac{2}{3})}^{2}$×$\frac{8}{15}$+${(2-\frac{2}{3})}^{2}$×$\frac{1}{15}$=$\frac{16}{45}$.
故答案为:$\frac{16}{45}$.
点评 本题考查了离散型随机变量的分布列、数学期望与方差的计算问题,是基础题.

练习册系列答案
相关题目
7.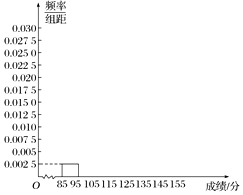 高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
(1)表格中①②③④处的数值分别为1、0.025、0.100、1.000;
(2)在图中画出[85,155]的频率分布直方图;
(3)根据题干信息估计总体平均数,并估计总体落在[125,155]上的频率.
 高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:| 分组 | 频数 | 频率 |
| [85,95) | ① | ② |
| [95,105) | 0.050 | |
| [105,115) | 0.200 | |
| [115,125) | 12 | 0.300 |
| [125,135) | 0.275 | |
| [135,145) | 4 | ③ |
| [145,155] | 0.050 | |
| 合计 | ④ |
(2)在图中画出[85,155]的频率分布直方图;
(3)根据题干信息估计总体平均数,并估计总体落在[125,155]上的频率.
4.定义在R上的函数y=f(x)满足:f(x)+f'(x)>1,f(0)=2018,则不等式exf(x)-ex>2017(其中e为自然对数的底数)的解集为( )
| A. | (2017,+∞) | B. | (-∞,0)∪(2017,+∞) | C. | (0,+∞) | D. | (-∞,0)∪(0,+∞) |
1.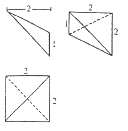 已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体最长的棱长度为( )
已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体最长的棱长度为( )
 已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体最长的棱长度为( )
已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体最长的棱长度为( )| A. | $2\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 3 | D. | $2\sqrt{3}$ |
2.在△ABC中,a,b,c分别是内角A,B,C的对边,若A=$\frac{2π}{3}$,b=$\sqrt{2}$,△ABC的面积为$\sqrt{3}$,则a的值为( ) )
| A. | $\sqrt{6}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{14}$ |
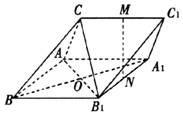 如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.
如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.