10.如图是“二分法”求方程近似解的流程图,在①,②处应填写的内容分别是( )
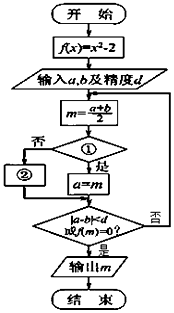

| A. | f(a)•f(m)<0?;b=m | B. | f(b)•f(m)<0?;b=m | C. | f(a)•f(m)<0?;m=b | D. | f(b)•f(m)<0?;b=m |
9.画边长为2的正方体ABCD-A1B1C1D1的三视图中的正视图时,若以△A1C1D所在的平面为投影面,则得到的正视图面积为( )
| A. | 2 | B. | $2\sqrt{3}$ | C. | 4 | D. | $4\sqrt{3}$ |
8.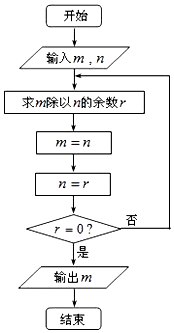 如图所示的程序框图描述的算法称为“欧几里得”辗转相除法,若输入m=2821,n=2015,则输出的m的值为( )
如图所示的程序框图描述的算法称为“欧几里得”辗转相除法,若输入m=2821,n=2015,则输出的m的值为( )
 如图所示的程序框图描述的算法称为“欧几里得”辗转相除法,若输入m=2821,n=2015,则输出的m的值为( )
如图所示的程序框图描述的算法称为“欧几里得”辗转相除法,若输入m=2821,n=2015,则输出的m的值为( )| A. | 1 | B. | 403 | C. | 806 | D. | 2015 |
5.已知$f(x)=\left\{{\begin{array}{l}{{{log}_{\frac{1}{16}}}({x+1}),x<0}\\{-{x^2}+x,x≥0}\end{array}}\right.$,则关于x的方程f(x)=m(m∈R)恰有三个不同的实数根a,b,c,则abc的取值范围是( )
| A. | $({-\frac{1}{16},0})$ | B. | $({-\frac{1}{4},0})$ | C. | $({-\frac{1}{8},0})$ | D. | $({-\frac{1}{2},0})$ |
4.已知函数f(x)是R上的奇函数,且满足f(π-x)=f(x),当0≤x≤$\frac{π}{2}$时,f(x)=cosx-1,则当0≤x≤π时,f(x)的图象与x轴所围成图形的面积为( )
| A. | π-2 | B. | 2π-4 | C. | 3π-6 | D. | 4π-8 |
3.已知函数g(x)=1-cos(πx+ϕ)(0≤ϕ<π)的图象过($\frac{1}{2}$,2),若有4个不同的正数xi满足g(xi)=M(0<M<1),且xi<4(i=1,2,3,4),则从这四个数中任意选出两个,它们的和不超过5的概率为( )
0 239831 239839 239845 239849 239855 239857 239861 239867 239869 239875 239881 239885 239887 239891 239897 239899 239905 239909 239911 239915 239917 239921 239923 239925 239926 239927 239929 239930 239931 239933 239935 239939 239941 239945 239947 239951 239957 239959 239965 239969 239971 239975 239981 239987 239989 239995 239999 240001 240007 240011 240017 240025 266669
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
