题目内容
9.画边长为2的正方体ABCD-A1B1C1D1的三视图中的正视图时,若以△A1C1D所在的平面为投影面,则得到的正视图面积为( )| A. | 2 | B. | $2\sqrt{3}$ | C. | 4 | D. | $4\sqrt{3}$ |
分析 在平面A1C1D中建立坐标系,求出正方体各点在此平面上的投影坐标即可得出投影面积.
解答 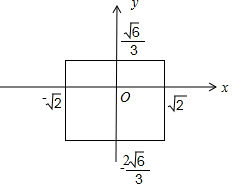 解:显然△A1C1D是边长为2$\sqrt{2}$的等边三角形,且BD1⊥平面A1C1D,
解:显然△A1C1D是边长为2$\sqrt{2}$的等边三角形,且BD1⊥平面A1C1D,
设垂直为O,则O为△A1C1D的中心,
由V${\;}_{{D}_{1}-{A}_{1}{C}_{1}D}$=V${\;}_{D-{A}_{1}{C}_{1}{D}_{1}}$得$\frac{1}{3}×\frac{\sqrt{3}}{4}×(2\sqrt{2})^{2}×O{D}_{1}$=$\frac{1}{3}×\frac{1}{2}×2×2×2$,
∴OD1=$\frac{2\sqrt{3}}{3}$,
以O为坐标原点,以A1C1的平行线为x轴,以DO为y轴,以OD1为z轴建立空间坐标系,如图所示: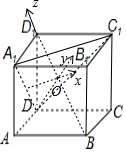
∴A在平面xoy上的投影为(-$\sqrt{2}$,-$\frac{2\sqrt{6}}{3}$),D在平面xoy上的投影为(0,-$\frac{2\sqrt{6}}{3}$),A1在平面xoy上的投影为(-$\sqrt{2}$,$\frac{\sqrt{6}}{3}$),
B1在平面xoy上的投影为(0,$\frac{\sqrt{6}}{3}$),C1在平面xoy上的投影为($\sqrt{2}$,$\frac{\sqrt{6}}{3}$),C在平面xoy上的投影为($\sqrt{2}$,-$\frac{2\sqrt{6}}{3}$),
∴正方体正视图的面积为S=2$\sqrt{2}$×$\sqrt{6}$=4$\sqrt{3}$.
故选:D.
点评 本题考查了空间几何体的应用问题,也考查了空间想象能力与逻辑推理能力的应用问题,

练习册系列答案
相关题目
20.若$\frac{1+mi}{1-i}$为纯虚数,则m的值为( )
| A. | m=-1 | B. | m=1 | C. | m=2 | D. | m=-2 |
17.已知f(x)=$\frac{a}{2}$-$\frac{3}{{2}^{x}+1}$是R上的奇函数,则f(a)的值为( )
| A. | $\frac{7}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
4.已知函数f(x)是R上的奇函数,且满足f(π-x)=f(x),当0≤x≤$\frac{π}{2}$时,f(x)=cosx-1,则当0≤x≤π时,f(x)的图象与x轴所围成图形的面积为( )
| A. | π-2 | B. | 2π-4 | C. | 3π-6 | D. | 4π-8 |
14.已知定义在R上的可导函数f(x)的导函数为f′(x),若对于任意实数x,有f(x)>f′(x),且y=f(x)-2为奇函数,则不等式f(x)<2ex的解集为( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,e2) | D. | (e2,+∞) |
19.已知双曲线与椭圆x2+$\frac{{y}^{2}}{2}$=1有公共焦点,且双曲线的离心率为$\sqrt{5}$,则该双曲线的渐近线方程为( )
| A. | y=±2x | B. | y=±$\frac{2\sqrt{5}}{5}$ | C. | y=±$\frac{\sqrt{5}}{2}$x | D. | y=±$\frac{1}{2}$x |