题目内容
5.已知$f(x)=\left\{{\begin{array}{l}{{{log}_{\frac{1}{16}}}({x+1}),x<0}\\{-{x^2}+x,x≥0}\end{array}}\right.$,则关于x的方程f(x)=m(m∈R)恰有三个不同的实数根a,b,c,则abc的取值范围是( )| A. | $({-\frac{1}{16},0})$ | B. | $({-\frac{1}{4},0})$ | C. | $({-\frac{1}{8},0})$ | D. | $({-\frac{1}{2},0})$ |
分析 作出f(x)的函数图象,根据图象判断a,b,c的范围和关系,利用基本不等式和不等式的性质得出abc的范围.
解答 解:作出f(x)的函数图象,如图所示: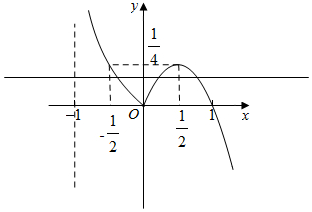
不妨设a<b<c,则-$\frac{1}{2}$<a<0$<b<\frac{1}{2}<1$,
由图象可知b,c关于直线x=$\frac{1}{2}$对称,
∴b+c=1,bc<($\frac{b+c}{2}$)2=$\frac{1}{4}$,
∴0<bc<$\frac{1}{4}$,又-$\frac{1}{2}<a<0$,
∴-$\frac{1}{8}$<abc<0.
故选C.
点评 本题考查了函数零点与函数图象的关系,不等式的性质,属于中档题.

练习册系列答案
相关题目
13.执行如图所示的程序框图,则输出s的值等于( )
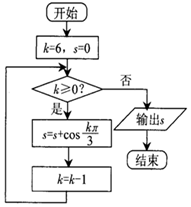

| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | 1 |
10.如图是“二分法”求方程近似解的流程图,在①,②处应填写的内容分别是( )
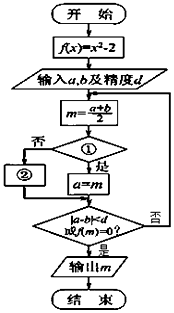

| A. | f(a)•f(m)<0?;b=m | B. | f(b)•f(m)<0?;b=m | C. | f(a)•f(m)<0?;m=b | D. | f(b)•f(m)<0?;b=m |
14.《孙子算经》是我国古代内容极为丰富的数学名著,其中一个问题的解答可以用如图的算法来实现,若输入的S,T的值分别为40,126,则输出a,b的值分别为( )
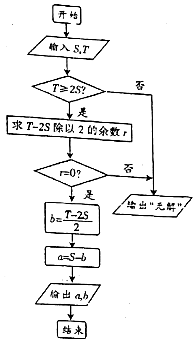

| A. | 17,23 | B. | 21,21 | C. | 19,23 | D. | 20,20 |