题目内容
10．如图是“二分法”求方程近似解的流程图，在①，②处应填写的内容分别是（ ）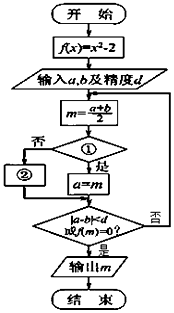
| A． | f（a）•f（m）＜0？；b=m | B． | f（b）•f（m）＜0？；b=m | C． | f（a）•f（m）＜0？；m=b | D． | f（b）•f（m）＜0？；b=m |
分析 根据二分法的定义结合程序框图的应用进行判断即可．
解答 解：根据二分法的定义知①f（b）•f（m）＜0？；②b=m，
故选：B
点评 本题主要考查程序框图的判断，结合二分法的定义是解决本题的关键．
练习册系列答案
相关题目
1．若f（x）是定义在R上的可导函数，且对任意x∈R，满足f（x）+f'（x）＞0，则对任意实数a，b（ ）
| A． | a＞b?eaf（b）＞ebf（a） | B． | a＞b?eaf（b）＜ebf（a） | C． | a＞b?eaf（a）＜ebf（b） | D． | a＞b?eaf（a）＞ebf（b） |
在△ABC中，∠B=$\frac{π}{6}$，AC=$\sqrt{5}$，D是AB边上一点，CD=2，△ACD的面积为2，∠ACD为锐角，则BC=$\frac{8\sqrt{5}}{5}$．
5．已知$f（x）=\left\{{\begin{array}{l}{{{log}_{\frac{1}{16}}}（{x+1}），x＜0}\\{-{x^2}+x，x≥0}\end{array}}\right.$，则关于x的方程f（x）=m（m∈R）恰有三个不同的实数根a，b，c，则abc的取值范围是（ ）
| A． | $（{-\frac{1}{16}，0}）$ | B． | $（{-\frac{1}{4}，0}）$ | C． | $（{-\frac{1}{8}，0}）$ | D． | $（{-\frac{1}{2}，0}）$ |
2．我国古代数学名著《九章算术》的论割圆术中有：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣．”它体现了一种无限与有限的转化过程．比如在表达式1+$\frac{1}{1+\frac{1}{1+…}}$中“…”即代表无数次重复，但原式却是个定值，它可以通过方程1+$\frac{1}{x}$=x求得x=$\frac{\sqrt{5}+1}{2}$．类比上述过程，则$\sqrt{3+2\sqrt{3+2\sqrt{…}}}$=（ ）
| A． | 3 | B． | $\frac{\sqrt{13}+1}{2}$ | C． | 6 | D． | 2$\sqrt{2}$ |
19．
已知全集U=R，集合A={x|x（x+2）＜0}，B={x||x|≤1}，则如图阴影部分表示的集合是（ ）
已知全集U=R，集合A={x|x（x+2）＜0}，B={x||x|≤1}，则如图阴影部分表示的集合是（ ）| A． | （-2，1） | B． | [-1，0]∪[1，2） | C． | （-2，-1）∪[0，1] | D． | [0，1] |