题目内容
4.已知函数f(x)是R上的奇函数,且满足f(π-x)=f(x),当0≤x≤$\frac{π}{2}$时,f(x)=cosx-1,则当0≤x≤π时,f(x)的图象与x轴所围成图形的面积为( )| A. | π-2 | B. | 2π-4 | C. | 3π-6 | D. | 4π-8 |
分析 根据函数的奇偶性得到函数的周期是2π,分别求出函数的解析式,利用积分的应用即可得到结论.
解答 解:由f(π-x)=f(x)得f(x+π)=f(-x)=-f(x),
当0≤x≤$\frac{π}{2}$,由已知得到f(x)=cosx-1,
∵f(x)是R上的奇函数,
∴当$\frac{π}{2}$<x≤π时,0<π-x≤$\frac{π}{2}$,
所以由f(π-x)=f(x)=cos(π-x)-1=-cosx-1,
所以f(x)=$\left\{\begin{array}{l}{cosx-1,0≤x≤\frac{π}{2}}\\{-cosx-1,\frac{π}{2}<x≤π}\end{array}\right.$,
所以当0≤x≤π时,f(x)的图象与x轴所围成图形的面积-${∫}_{0}^{\frac{π}{2}}(cosx-1)dx+{∫}_{\frac{π}{2}}^{π}(-cosx-1)dx$=${∫}_{0}^{\frac{π}{2}}(1-cosx)dx+{∫}_{\frac{π}{2}}^{π}(cosx+1)dx$=(x-sinx)|${\;}_{0}^{\frac{π}{2}}$+(sinx+x)|${\;}_{\frac{π}{2}}^{π}$=π-2;
故选A.
点评 本题主要考查利用积分求面积,根据函数的奇偶性和周期性分别求出对应的解析式是解决本题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
15.我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径.“开立圆术”相当于给出了已知球的体积V,求其直径d的一个近似公式$d≈\root{3}{{\frac{16}{3}V}}$,人们还用过一些类似的近似公式,根据π=3.14159…判断,下列近似公式中最精确的一个是( )
| A. | $d≈\root{3}{{\frac{60}{31}V}}$ | B. | $d≈\root{3}{2V}$ | C. | $d≈\root{3}{{\frac{15}{8}V}}$ | D. | $d≈\root{3}{{\frac{21}{11}V}}$ |
19.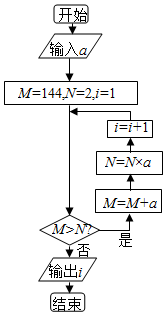 执行如图所示的程序框图,若输出的i=3,则输入的a(a>0)的取值范围是( )
执行如图所示的程序框图,若输出的i=3,则输入的a(a>0)的取值范围是( )
 执行如图所示的程序框图,若输出的i=3,则输入的a(a>0)的取值范围是( )
执行如图所示的程序框图,若输出的i=3,则输入的a(a>0)的取值范围是( )| A. | [9,+∞) | B. | [8,9] | C. | [8,144) | D. | [9,144) |
9.画边长为2的正方体ABCD-A1B1C1D1的三视图中的正视图时,若以△A1C1D所在的平面为投影面,则得到的正视图面积为( )
| A. | 2 | B. | $2\sqrt{3}$ | C. | 4 | D. | $4\sqrt{3}$ |