9.执行如图所示的程序框图,输出S的值等于( )
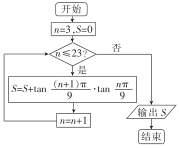

| A. | $-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-21$ | B. | $\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-22$ | ||
| C. | $-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-22$ | D. | $\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-21$ |
8.有甲、乙两个班级进行数学考试,按照大于等于120分为优秀,120分以下为非优秀统计成绩后,得到如下2×2列联表:(单位:人).
已知在全部105人中随机抽取1人成绩是优秀的概率为$\frac{2}{7}$,
(1)请完成上面的2 x×2列联表,并根据表中数据判断,是否有95%的把握认为“成绩与班级有关系”?
(2)若甲班优秀学生中有男生6名,女生4名,现从中随机选派3名学生参加全市数学竞赛,记参加竞赛的男生人数为X,求X的分布列与期望.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 总计 | 105 |
(1)请完成上面的2 x×2列联表,并根据表中数据判断,是否有95%的把握认为“成绩与班级有关系”?
(2)若甲班优秀学生中有男生6名,女生4名,现从中随机选派3名学生参加全市数学竞赛,记参加竞赛的男生人数为X,求X的分布列与期望.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 6.635 |
6.已知过曲线$\left\{\begin{array}{l}{x=3sinθ}\\{y=3cosθ}\end{array}\right.$(θ为参数,0≤θ≤π)上一点P与原点O的直线PO的倾斜角为$\frac{π}{2}$,则P点坐标是( )
| A. | (0,3) | B. | $(-\frac{12}{5},-\frac{12}{5})$ | C. | (-3,0) | D. | $(\frac{12}{5},\frac{12}{5})$ |
3.在△ABC中,$∠ACB=\frac{π}{6},BC=\sqrt{3},AC=4$,则AB等于( )
0 239829 239837 239843 239847 239853 239855 239859 239865 239867 239873 239879 239883 239885 239889 239895 239897 239903 239907 239909 239913 239915 239919 239921 239923 239924 239925 239927 239928 239929 239931 239933 239937 239939 239943 239945 239949 239955 239957 239963 239967 239969 239973 239979 239985 239987 239993 239997 239999 240005 240009 240015 240023 266669
| A. | $\sqrt{7}$ | B. | 3 | C. | $\sqrt{11}$ | D. | $\sqrt{13}$ |
 已知A,B分别是射线CM,CM(不含端点C)上运动,在△ABC中,角A,B,C所对的边分别为a,b,c.
已知A,B分别是射线CM,CM(不含端点C)上运动,在△ABC中,角A,B,C所对的边分别为a,b,c.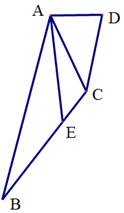 在四边形ABCD中,点E在BC上,∠BAD=$\frac{2π}{3}$,AD:AC:CD=1:2:$\sqrt{3}$.
在四边形ABCD中,点E在BC上,∠BAD=$\frac{2π}{3}$,AD:AC:CD=1:2:$\sqrt{3}$.