��Ŀ����
11������������ת������ѧ��һ����Ҫ˼�뷽�������ڡ�����������������Բ����������ע���У�����֮�ָ������ڲ��ɸ����Բ���������ʧ�ӣ���˵������Բ������һ������������ת�����̣�����$\sqrt{2+\sqrt{2+\sqrt{2+��}}}$�С����������������ظ�����ԭʽȴ�Ǹ���ֵx�������ͨ������$\sqrt{2+x}$=xȷ������x=2�����Ƶؿ���ѭ��С����Ϊ��������0.$\stackrel{•}{3}\stackrel{•}{6}$��Ϊ�����Ľ��Ϊ$\frac{4}{11}$������ ������������0.$\stackrel{•}{3}\stackrel{•}{6}$=x����ɵõ�����0.36+$\frac{1}{100}$x=x����ü��ɣ�
��� �⣺��0.$\stackrel{•}{3}\stackrel{•}{6}$=x����0.00$\stackrel{•}{3}\stackrel{•}{6}$=$\frac{1}{100}$x��
��0.36+$\frac{1}{100}$x=x��
���x=$\frac{4}{11}$��
�ʴ�Ϊ��$\frac{4}{11}$
���� ���⿼����������������⣬��һ�������⣮

��ϰ��ϵ�д�
 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
�����Ŀ
1��������R�ϵĺ���f��x���ĵ�����Ϊf'��x������f��x��+xf'��x����xf��x����x��R�������������
| A�� | $\frac{2}{e}f��2����f��1��$ | B�� | $\frac{2}{e}f��2����f��1��$ | C�� | f��1����0 | D�� | f��-1����0 |
6����֪������$\left\{\begin{array}{l}{x=3sin��}\\{y=3cos��}\end{array}\right.$����Ϊ������0�ܦȡܦУ���һ��P��ԭ��O��ֱ��PO����б��Ϊ$\frac{��}{2}$����P�������ǣ�������
| A�� | ��0��3�� | B�� | $��-\frac{12}{5}��-\frac{12}{5}��$ | C�� | ��-3��0�� | D�� | $��\frac{12}{5}��\frac{12}{5}��$ |
16����ͼ��ij�����������ͼ����ֱ�������Σ��������������ⳤΪ2����ü����������������ǣ�������
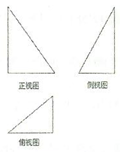

| A�� | $\sqrt{6}��$ | B�� | $\frac{4}{3}��$ | C�� | 4�� | D�� | 6�� |
3����֪����g��x��=1-cos����x+ϕ����0��ϕ���У���ͼ�����$\frac{1}{2}$��2��������4����ͬ������xi����g��xi��=M��0��M��1������xi��4��i=1��2��3��4����������ĸ���������ѡ�����������ǵĺͲ�����5�ĸ���Ϊ��������
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{2}{3}$ |
20����f��x���Ƕ�����R�ϵ��溯������x��0ʱ��f��x��=2x+1����f��0��+f��1��=��������
| A�� | $-\frac{3}{2}$ | B�� | 1 | C�� | $\frac{1}{2}$ | D�� | 5 |
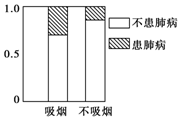 ������ͼ��ʾ�ĵȸ�����ͼ�ش������뻼�β��й�ϵ�������С���û�С���
������ͼ��ʾ�ĵȸ�����ͼ�ش������뻼�β��й�ϵ�������С���û�С���