题目内容
9.执行如图所示的程序框图,输出S的值等于( )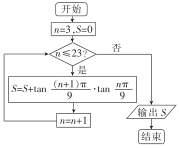
| A. | $-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-21$ | B. | $\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-22$ | ||
| C. | $-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-22$ | D. | $\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-21$ |
分析 模拟执行程序框图知该程序的功能是计算并输出
S=tan$\frac{4π}{9}$•tan$\frac{3π}{9}$+tan$\frac{5π}{9}$•tan$\frac{4π}{9}$+…+tan$\frac{24π}{9}$•tan$\frac{23π}{9}$的值,
由两角差的正切值公式计算S的值即可.
解答 解:模拟执行如图所示的程序框图知,
该程序的功能是计算并输出
S=tan$\frac{4π}{9}$•tan$\frac{3π}{9}$+tan$\frac{5π}{9}$•tan$\frac{4π}{9}$+…+tan$\frac{24π}{9}$•tan$\frac{23π}{9}$的值,
则S=(1+tan$\frac{4π}{9}$tan$\frac{3π}{9}$)+(1+tan$\frac{5π}{9}$tan$\frac{4π}{9}$)+…+(1+tan$\frac{24π}{9}$tan$\frac{23π}{9}$)-21
=$\frac{tan\frac{4π}{9}-tan\frac{3π}{9}}{tan(\frac{4π}{9}-\frac{3π}{9})}$+$\frac{tan\frac{5π}{9}-tan\frac{4π}{9}}{tan(\frac{5π}{9}-\frac{4π}{9})}$+…+$\frac{tan\frac{24π}{9}-tan\frac{23π}{9}}{tan(\frac{24π}{9}-\frac{23π}{9})}$-21
=$\frac{tan\frac{24π}{9}-tan\frac{3π}{9}}{tan\frac{π}{9}}$-21
=$\frac{tan\frac{8π}{3}-tan\frac{π}{3}}{tan\frac{π}{9}}$-21
=$\frac{-2\sqrt{3}}{tan\frac{π}{9}}$-21.
故选:A.
点评 本题考查了程序框图与两角差的正切公式应用问题,是综合题.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案| 无促销活动 | 采用促销方案1 | 采用促销方案2 | ||
| 本年度平均销售额不高于上一年度平均销售额 | 48 | 11 | 31 | 90 |
| 本年度平均销售额高于上一年度平均销售额 | 52 | 69 | 29 | 150 |
| 100 | 80 | 60 |
(Ⅱ)已知该公司产品的成本为10元/件(未包括促销活动运作费用),为制定本年度该地区的产品销售价格,统计上一年度的8组售价xi(单位:元/件,整数)和销量yi(单位:件)(i=1,2,…8)如表所示:
| 售价x | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
| 销量y | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
(ⅱ)根据所选回归模型,分析售价x定为多少时?利润z可以达到最大.
| $\hat y=-1200lnx+5000$ | $\hat y=-27x+1700$ | $\hat y=-\frac{1}{3}{x^2}+1200$ | |
| $\sum_{i=1}^8{({y_i}}-{\hat y_i}{)^2}$ | 49428.74 | 11512.43 | 175.26 |
| $\sum_{i=1}^8{({y_i}}-\overline y{)^2}$ | 124650 | ||
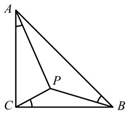 如图,在等腰直角三角形ABC中,∠C是直角,P是三角形内部一点,且∠CAP=∠BCP=∠ABP=α,则tanα的值等于( )
如图,在等腰直角三角形ABC中,∠C是直角,P是三角形内部一点,且∠CAP=∠BCP=∠ABP=α,则tanα的值等于( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
| A. | [-$\frac{\sqrt{3}}{3}$,0] | B. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] | C. | [0,$\frac{\sqrt{3}}{3}$] | D. | (-∞,$\frac{\sqrt{3}}{3}$] |
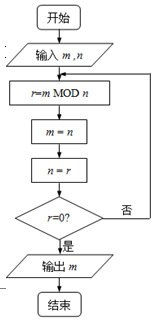 右边程序框图的算法思路源于数学名著《几何原本》中的“辗转
右边程序框图的算法思路源于数学名著《几何原本》中的“辗转