题目内容
4．在△ABC中，a=2，b=3，C=120°，求边c的大小及△ABC的面积．分析 先由余弦定理求出$c=\sqrt{19}$，再由正弦定理能求出△ABC的面积．
解答 解：因为a=2，b=3，C=120°，
所以c2=a2+b2-2abcosC=19，
所以$c=\sqrt{19}$，
所以${S_{△ABC}}=\frac{1}{2}absinC=\frac{1}{2}×2×3sin{120°}=\frac{{3\sqrt{3}}}{2}$．
点评 本题考查三角形的边长及三角形面积的求法，涉及到正弦定理、余弦定理等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14．曲线$\left\{\begin{array}{l}{x=sinθ}\\{y=cos2θ}\end{array}\right.$（θ参数）在y轴上的截距为（ ）
| A． | 、$-\frac{1}{2}$ | B． | -1 | C． | $\frac{1}{2}$ | D． | 1 |
12．设$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$均为非零向量，若|（$\overrightarrow{a}$+$\overrightarrow{b}$）•$\overrightarrow{c}$|=|（$\overrightarrow{a}$-$\overrightarrow{b}$）•$\overrightarrow{c}$|，则（ ）
| A． | $\overrightarrow{a}$∥$\overrightarrow{b}$ | B． | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | C． | $\overrightarrow{a}$∥$\overrightarrow{c}$或$\overrightarrow{b}$∥$\overrightarrow{c}$ | D． | $\overrightarrow{a}$⊥$\overrightarrow{c}$或$\overrightarrow{b}$⊥$\overrightarrow{c}$ |
9．执行如图所示的程序框图，输出S的值等于（ ）
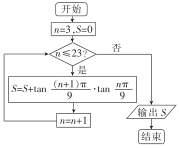
| A． | $-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-21$ | B． | $\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-22$ | ||
| C． | $-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-22$ | D． | $\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-21$ |
16．如图，某几何体的三视图都是直角三角形，若几何体的最大棱长为2，则该几何体的外接球的体积是（ ）
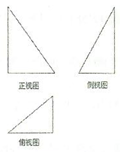
| A． | $\sqrt{6}π$ | B． | $\frac{4}{3}π$ | C． | 4π | D． | 6π |
13．
如图，若程序框图运行后输出的结果是57，则判断框中应填入的条件是（ ）
如图，若程序框图运行后输出的结果是57，则判断框中应填入的条件是（ ）| A． | A＜4 | B． | A＜5 | C． | A≤5 | D． | A≤6 |