题目内容
8.有甲、乙两个班级进行数学考试,按照大于等于120分为优秀,120分以下为非优秀统计成绩后,得到如下2×2列联表:(单位:人).| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 总计 | 105 |
(1)请完成上面的2 x×2列联表,并根据表中数据判断,是否有95%的把握认为“成绩与班级有关系”?
(2)若甲班优秀学生中有男生6名,女生4名,现从中随机选派3名学生参加全市数学竞赛,记参加竞赛的男生人数为X,求X的分布列与期望.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 6.635 |
分析 (1)由已知填写列联表,计算观测值,对照临界值即可得出结论;
(2)根据题意知X的所有可能值,计算对应的概率,写出随机变量X的分布列,计算数学期望值.
解答 解:(1)由已知,两个班的优秀学生人数为105×$\frac{2}{7}$=30,填写2×2列联表如下;
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | 45 | 55 |
| 乙班 | 20 | 30 | 50 |
| 总计 | 30 | 75 | 105 |
所以有95%的把握认为“成绩与班级有关系”;
(2)根据题意,X的所有可能取值为0,1,2,3;
计算P(X=0)=$\frac{{C}_{4}^{3}}{{C}_{10}^{3}}$=$\frac{4}{120}$=$\frac{1}{30}$,
P(X=1)=$\frac{{C}_{6}^{1}{•C}_{4}^{2}}{{C}_{10}^{3}}$=$\frac{36}{120}$=$\frac{3}{10}$,
P(X=2)=$\frac{{C}_{6}^{2}{•C}_{4}^{1}}{{C}_{10}^{3}}$=$\frac{60}{120}$=$\frac{1}{2}$,
P(X=3)=$\frac{{C}_{6}^{3}}{{C}_{10}^{3}}$=$\frac{1}{6}$;
∴随机变量X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{30}$ | $\frac{3}{10}$ | $\frac{1}{2}$ | $\frac{1}{6}$ |
或X服从超几何分布,且N=10,M=6,n=3,
所以E(X)=$\frac{nM}{N}$=$\frac{3×6}{10}$=$\frac{9}{5}$.
点评 本题考查了独立性检验与离散型随机变量的分布列和数学期望的计算问题,是中档题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
3.在△ABC中,$∠ACB=\frac{π}{6},BC=\sqrt{3},AC=4$,则AB等于( )
| A. | $\sqrt{7}$ | B. | 3 | C. | $\sqrt{11}$ | D. | $\sqrt{13}$ |
13.执行如图所示的程序框图,则输出s的值等于( )
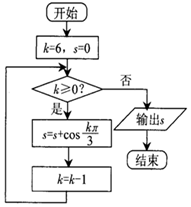

| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | 1 |