18.已知R为实数集,集合A={x|x2-2x≥0},B={x|x>1},则(∁RA)∩B( )
| A. | (0,1) | B. | (0,1] | C. | (1,2) | D. | (1,2] |
16.“¬p为真”是“p∨q为假”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
13.已知实数a>0,函数$f(x)=\left\{\begin{array}{l}{e^{x-1}}+\frac{a}{2},x<0\\{e^{x-1}}+\frac{a}{2}{x^2}-(a+1)x+\frac{a}{2},x≥0\end{array}\right.$,若关于x的方程$f[-f(x)]={e^{-a}}+\frac{a}{2}$有三个不等的实根,则实数a的取值范围是( )
| A. | $(1,2+\frac{2}{e})$ | B. | $(2,2+\frac{2}{e})$ | C. | $(1,1+\frac{1}{e})$ | D. | $(2,2+\frac{1}{e})$ |
12.已知双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$上有不共线三点A,B,C,且AB,BC,AC的中点分别为D,E,F,若满足OD,OE,OF的斜率之和为-1,则$\frac{1}{{{k_{AB}}}}+\frac{1}{{{k_{BC}}}}+\frac{1}{{{k_{AC}}}}$=( )
| A. | 2 | B. | $-\sqrt{3}$ | C. | -2 | D. | 3 |
11.定义在R上的奇函数f(x)满足f(x-2)=f(x+2),且当x∈[-2,0]时,f(x)=3x-1,则f(9)=( )
| A. | -2 | B. | 2 | C. | $-\frac{2}{3}$ | D. | $\frac{2}{3}$ |
10.若O为坐标原点,已知实数x,y满足条件$\left\{\begin{array}{l}x+y≥1\\ x-y≥-1\\ 2x-y≤2\end{array}\right.$,在可行域内任取一点P(x,y),则|OP|的最小值为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{3}{2}$ |
9.已知向量$\overrightarrow m=(1,2)$,$\overrightarrow n=(2,3)$,则$\overrightarrow m$在$\overrightarrow n$方向上的投影为( )
0 239748 239756 239762 239766 239772 239774 239778 239784 239786 239792 239798 239802 239804 239808 239814 239816 239822 239826 239828 239832 239834 239838 239840 239842 239843 239844 239846 239847 239848 239850 239852 239856 239858 239862 239864 239868 239874 239876 239882 239886 239888 239892 239898 239904 239906 239912 239916 239918 239924 239928 239934 239942 266669
| A. | $\sqrt{13}$ | B. | 8 | C. | $\frac{{8\sqrt{5}}}{5}$ | D. | $\frac{{8\sqrt{13}}}{13}$ |
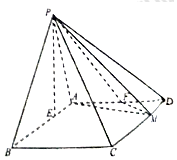 在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,$AD=2\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.
在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,$AD=2\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.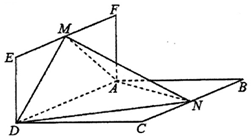 如图,平面ABCD⊥平面ADEF,四边形ABCD为菱形,四边形ADEF为矩形,M,N分别是EF,BC的中点,AB=2AF,∠CBA=
如图,平面ABCD⊥平面ADEF,四边形ABCD为菱形,四边形ADEF为矩形,M,N分别是EF,BC的中点,AB=2AF,∠CBA=