题目内容
16．“￢p为真”是“p∨q为假”的（ ）条件．| A． | 充分不必要 | B． | 必要不充分 | ||
| C． | 充要 | D． | 既不充分也不必要 |
分析 根据复合命题真假关系，结合充分条件和必要条件的定义进行判断即可．
解答 解：￢p为真，则p为假命题，则当q为真命题时，p∨q为真命题，则充分性不成立，
若p∨q为假，则p，q同时为假命题，则￢p为真命题，即必要性成立，
则“￢p为真”是“p∨q为假”的必要不充分条件，
故选：B
点评 本题主要考查充分条件和必要条件的判断，结合充分条件和必要条件的定义是解决本题的关键．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
4．已知点P在双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$上，点A满足$\overrightarrow{PA}=（t-1）\overrightarrow{OP}$（t∈R），且$\overrightarrow{OA}•\overrightarrow{OP}=64$，$\overrightarrow{OB}=（0，1）$，则$|{\overrightarrow{OB}•\overrightarrow{OA}}|$的最大值为（ ）
| A． | $\frac{5}{4}$ | B． | $\frac{24}{5}$ | C． | $\frac{4}{5}$ | D． | $\frac{5}{24}$ |
11．定义在R上的奇函数f（x）满足f（x-2）=f（x+2），且当x∈[-2，0]时，f（x）=3x-1，则f（9）=（ ）
| A． | -2 | B． | 2 | C． | $-\frac{2}{3}$ | D． | $\frac{2}{3}$ |
1．在复平面中，复数$\frac{1}{{{{（{1+i}）}^2}+1}}+i$对应的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
2．
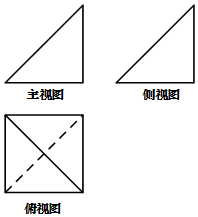某空间几何体的三视图如图所示，图中主视图和侧视图是两个全等的等腰直角三角形，腰长为4，俯视图中的四边形为正方形，则这个几何体的体积是（ ）
某空间几何体的三视图如图所示，图中主视图和侧视图是两个全等的等腰直角三角形，腰长为4，俯视图中的四边形为正方形，则这个几何体的体积是（ ）| A． | $\frac{32}{3}$ | B． | $\frac{64}{3}$ | C． | 16 | D． | 32 |