题目内容
17.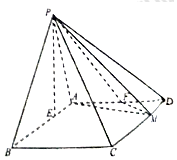 在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,$AD=2\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.
在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,$AD=2\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.(1)当$λ=\frac{2}{3}$时,证明:平面PFM⊥平面PAB;
(2)当$λ=\frac{1}{3}$时,求平面PAM与平面ABCD所成的二面角的正弦值及四棱锥P-ABCM的体积.
分析 (1)利用余弦定理计算FM,根据勾股定理得出FM⊥DM,即FM⊥AB,结合FM⊥PE得出FM⊥平面PAB,故平面PFM⊥平面PAB;
(2)AM⊥平面PAB,故∠PAB为二面角的平面角,求出AM,代入体积公式计算即可.
解答  解:(1)证明:当λ=$\frac{2}{3}$时,DM=$\frac{1}{3}$CD=$\frac{1}{3}$AB=1,
解:(1)证明:当λ=$\frac{2}{3}$时,DM=$\frac{1}{3}$CD=$\frac{1}{3}$AB=1,
又DF=$\frac{1}{2}$AD=$\sqrt{2}$,∠ADC=∠ABC=45°,
∴FM=$\sqrt{F{D}^{2}+D{M}^{2}-2FD•DM•cos45°}$=1,
∴FM2+DM2=FD2,
∴FM⊥DM.又DM∥AB,
∴FM⊥AB,
∵PE⊥平面ABCD,FM?平面ABCD,
∴PE⊥FM,PE∩AB=E,
∴FM⊥平面PAB,又FM?平面PFM,
∴平面PDM⊥平面PAB.
(2)当$λ=\frac{1}{3}$时,由(1)可知AM⊥平面PAB,
∴AM⊥AB,AM⊥PA,
∴∠PAB为二面角P-AM-B的平面角,
∵PA=$\sqrt{P{E}^{2}+A{E}^{2}}$=$\sqrt{5}$,
∴sin∠PAB=$\frac{PE}{PA}$=$\frac{2}{\sqrt{5}}$=$\frac{{2\sqrt{5}}}{5}$.
在△ADM中,由余弦定理得AM=$\sqrt{8+4-2•2\sqrt{2}•2•\frac{\sqrt{2}}{2}}$=2,
∴S梯形ABCM=$\frac{1}{2}$(1+3)×2=4,
∴${V_{P-ABCM}}=\frac{1}{3}{S_{梯形ABCD}}×PE=\frac{8}{3}$.
点评 本题考查了线面垂直的判定,面面垂直的判定,棱锥的体积计算,属于中档题.

| A. | 4 | B. | 3 | C. | 1 | D. | 2 |
| A. | 2 | B. | $-\sqrt{3}$ | C. | -2 | D. | 3 |
| A. | $(0,\frac{π}{6}]$ | B. | $[\frac{π}{3},\frac{π}{2}]$ | C. | $(0,\frac{π}{3}]$ | D. | $[\frac{π}{3},π)$ |
 已知空间几何体CBEADF如图所示,底面AEFD为矩形,平面BEFC⊥平面AEFD,∠CFE=∠BEF=90°,其中AE+BE=AD=2,DF+CF=4.
已知空间几何体CBEADF如图所示,底面AEFD为矩形,平面BEFC⊥平面AEFD,∠CFE=∠BEF=90°,其中AE+BE=AD=2,DF+CF=4.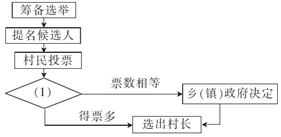 选举时常用的选举方式是差额选举(候选人多于当选人数),某村选举村长,具体方法是:筹备选举,由乡(镇)政府提名候选人,村民投票(同意,不同意,弃权),验票统计,得票多者选为村长;若票数相等,则由乡(镇)政府决定谁当选.下面的流程图表示该选举过程,则图(1)处应填的是验票统计.
选举时常用的选举方式是差额选举(候选人多于当选人数),某村选举村长,具体方法是:筹备选举,由乡(镇)政府提名候选人,村民投票(同意,不同意,弃权),验票统计,得票多者选为村长;若票数相等,则由乡(镇)政府决定谁当选.下面的流程图表示该选举过程,则图(1)处应填的是验票统计.