题目内容
11.定义在R上的奇函数f(x)满足f(x-2)=f(x+2),且当x∈[-2,0]时,f(x)=3x-1,则f(9)=( )| A. | -2 | B. | 2 | C. | $-\frac{2}{3}$ | D. | $\frac{2}{3}$ |
分析 根据题意,由f(x-2)=f(x+2),分析可得f(x)=f(x+4),即可得函数f(x)的周期为4,则有f(9)=f(1),由函数的解析式以及奇偶性可得f(1)的值,即可得答案.
解答 解:根据题意,函数f(x)满足f(x-2)=f(x+2),即f(x)=f(x+4),
则函数f(x)的周期为4,
f(9)=f(1),
又由函数f(x)为奇函数,则f(1)=-f(-1),
又由当x∈[-2,0]时,f(x)=3x-1,
则f(-1)=3-1-1=$\frac{1}{3}$-1=-$\frac{2}{3}$;
则有f(9)=f(1)=-f(-1)=$\frac{2}{3}$;
故选:D.
点评 本题考查函数奇偶性、周期性的应用,注意分析得到函数的周期.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
1.把8个相同的小球全部放入编号为1,2,3,4的四个盒中,则不同的放法数为( )
| A. | 35 | B. | 70 | C. | 165 | D. | 1860 |
19.某人午觉醒来,发现表停了,他打开收音机,想听电台报时,则他等待时间大于10分钟的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{10}$ | D. | $\frac{9}{10}$ |
16.“¬p为真”是“p∨q为假”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
3.已知函数$f(x)=\left\{\begin{array}{l}{e^{mx}}(x≥0)\\ \frac{1}{m}ln(-x)(x<0)\end{array}\right.$(其中m>0,e为自然对数的底数)的图象为曲线M,若曲线M上存在关于直线x=0对称的点,则实数m的取值范围是( )
| A. | $m≥\frac{1}{e}$ | B. | $0<m≤\frac{1}{e}$ | C. | $m≥\frac{1}{e^2}$ | D. | $0<m≤\frac{1}{e^2}$ |
20.在平面直角坐标系中,O为坐标原点,A(-1,2),B(3,4),C为AB中点,则$\overrightarrow{AB}$•$\overrightarrow{OC}$的值是( )
| A. | 10 | B. | -10 | C. | 20 | D. | -20 |
17.某几何体的三视图如图所示,则该几何体的表面积为( )
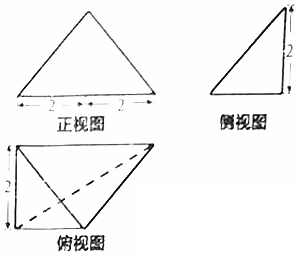

| A. | $6+4\sqrt{2}+2\sqrt{6}$ | B. | $4+6\sqrt{2}+2\sqrt{5}$ | C. | $4+2\sqrt{5}+2\sqrt{6}$ | D. | $4+6\sqrt{2}+2\sqrt{6}$ |