Question

13．已知实数a＞0，函数$f（x）=\left\{\begin{array}{l}{e^{x-1}}+\frac{a}{2}，x＜0\\{e^{x-1}}+\frac{a}{2}{x^2}-（a+1）x+\frac{a}{2}，x≥0\end{array}\right.$，若关于x的方程$f[-f（x）]={e^{-a}}+\frac{a}{2}$有三个不等的实根，则实数a的取值范围是（　　）

• A． $（1，2+\frac{2}{e}）$
• B． $（2，2+\frac{2}{e}）$
• C． $（1，1+\frac{1}{e}）$
• D． $（2，2+\frac{1}{e}）$

Answer 1

分析 求出f（x）=e^-a+$\frac{a}{2}$的解为1-a，即可得出f（x）=a-1有三解，判断f（x）的单调性，计算最值，作出f（x）的图象，根据图象得出关于a的不等式，即可解出a的范围．

解答 解：当x＜0时，f（x）在（-∞，0）上单调递增，且x→-∞时，f（x）→$\frac{a}{2}$，
当x≥0时，f′（x）=e^x-1+ax-a-1，
∴f′（x）是增函数，且f′（1）=0，
∴当0＜x＜1时，f′（x）＜0，当x＞1时，f′（x）＞0，
∴f（x）在（0，1）上单调递减，在（1，+∞）上单调递增，
又f（1）=0，当x→+∞时，f（x）→+∞，
作出f（x）的大致函数图象如图所示：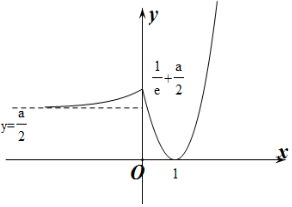

由图象可知f（x）≥0，∴f（-f（x））∈（$\frac{a}{2}$，$\frac{1}{e}+\frac{a}{2}$]，
∴$\frac{a}{2}$＜e^-a+$\frac{a}{2}$≤$\frac{1}{e}$+$\frac{a}{2}$，
解得a≥1．
令-f（x）=t，则t≤0，且f（t）=e^-a+$\frac{a}{2}$，
由图象可知：f（t）=e^-a+$\frac{a}{2}$有三解，不妨设从小到大依次为t₁，t₂，t₃，
则t₁=1-a，t₃＞1＞t₂＞0不符合题意，舍去．
∴-f（x）=1-a，即f（x）=a-1．
∴f（x）=a-1有三解，
∴$\frac{a}{2}＜a-1＜\frac{1}{e}+\frac{a}{2}$，解得2$＜a＜2+\frac{2}{e}$．
故选B．

点评 本题考查了函数零点与函数图象的关系，函数单调性的判断与极值计算，属于中档题．