20.某学校食堂在高一年级学生中抽查了100名学生进行饮食习惯调查,结果如表:
(I)从这100人中随机抽取1人,求抽到喜欢吃辣的学生概率;
(II)试判断有多大把握认为喜欢吃辣与性别有关;
(III)已知在被调查的学生中有5人来自一班,其中有2人喜欢吃辣,从这5人中随机抽取3人,求其中恰有1人喜欢吃辣的概率.
下面临界值表仅供参考:
$({参考公式:{K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}},其中n=a+b+c+d})$.
0 239242 239250 239256 239260 239266 239268 239272 239278 239280 239286 239292 239296 239298 239302 239308 239310 239316 239320 239322 239326 239328 239332 239334 239336 239337 239338 239340 239341 239342 239344 239346 239350 239352 239356 239358 239362 239368 239370 239376 239380 239382 239386 239392 239398 239400 239406 239410 239412 239418 239422 239428 239436 266669
| 喜欢吃辣 | 不喜欢吃辣 | 合计 | |
| 男生 | 30 | 10 | 40 |
| 女生 | 25 | 35 | 60 |
| 合计 | 55 | 45 | 100 |
(II)试判断有多大把握认为喜欢吃辣与性别有关;
(III)已知在被调查的学生中有5人来自一班,其中有2人喜欢吃辣,从这5人中随机抽取3人,求其中恰有1人喜欢吃辣的概率.
下面临界值表仅供参考:
| P(K2≥k0) | 0.15 | 100. | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 8411. | 5.024 | 6.635 | 7.879 | 10.828 |
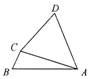 如图,在四边形ABCD中,∠B=$\frac{π}{3}$,∠BCA=2∠CAD,CD=2$\sqrt{2}$,AD=AC=4,则AB=$\sqrt{21}$.
如图,在四边形ABCD中,∠B=$\frac{π}{3}$,∠BCA=2∠CAD,CD=2$\sqrt{2}$,AD=AC=4,则AB=$\sqrt{21}$.