题目内容
19.已知tanα=$\frac{1}{3}$,则cos2α=$\frac{4}{5}$.分析 利用“弦化切”的思想,将cos2α=cos2α-sin2α=$\frac{1-ta{n}^{2}α}{1+ta{n}^{2}α}$,即可求解.
解答 解:由题意,tanα=$\frac{1}{3}$,
cos2α=cos2α-sin2α=$\frac{co{s}^{2}α-si{n}^{2}α}{co{s}^{2}α+si{n}^{2}α}$
=$\frac{1-ta{n}^{2}α}{1+ta{n}^{2}α}$=$\frac{1-\frac{1}{9}}{1+\frac{1}{9}}=\frac{4}{5}$.
故答案为$\frac{4}{5}$.
点评 本题主要考查了二倍角公式和同角三角函数关系式的计算.属于基础题

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
9.若从集合{1,2,3,4,5}中随机地选出三个元素,则满足其中两个元素的和等于第三个元素的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
7.设a,b是两条直线,α,β是两个平面,则a∥b的一个充分条件是( )
| A. | a⊥α,b∥β,α⊥β | B. | a?α,b⊥β,α∥β | C. | a⊥α,b⊥β,α∥β | D. | a?α,b∥β,α⊥β |
4.${(2x-\frac{1}{2x})^{10}}$的常数项为( )
| A. | -252 | B. | 252 | C. | -210 | D. | 210 |
11.设集合A={x|x2-1<0},B={x|y=ln(x-1)},则A∪B=( )
| A. | (-1,1) | B. | (-1,+∞) | C. | (-1,1)∪(1,+∞) | D. | (1,+∞) |
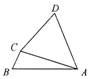 如图,在四边形ABCD中,∠B=$\frac{π}{3}$,∠BCA=2∠CAD,CD=2$\sqrt{2}$,AD=AC=4,则AB=$\sqrt{21}$.
如图,在四边形ABCD中,∠B=$\frac{π}{3}$,∠BCA=2∠CAD,CD=2$\sqrt{2}$,AD=AC=4,则AB=$\sqrt{21}$.