题目内容
14.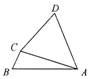 如图,在四边形ABCD中,∠B=$\frac{π}{3}$,∠BCA=2∠CAD,CD=2$\sqrt{2}$,AD=AC=4,则AB=$\sqrt{21}$.
如图,在四边形ABCD中,∠B=$\frac{π}{3}$,∠BCA=2∠CAD,CD=2$\sqrt{2}$,AD=AC=4,则AB=$\sqrt{21}$.
分析 设∠CAD=θ,则∠BCA=2θ,根据余弦定理求出cosθ,再根据同角的三角函数的关系和二倍角公式求出sin2θ,再由正弦定理即可求出.
解答 解:设∠CAD=θ,则∠BCA=2θ
在△ADC中,由余弦定理可得cosθ=$\frac{A{D}^{2}+A{C}^{2}-C{D}^{2}}{2AD•AC}$=$\frac{16+16-8}{2×4×4}$=$\frac{3}{4}$,
∴sinθ=$\sqrt{1-co{s}^{2}θ}$=$\frac{\sqrt{7}}{4}$,
∴sin2θ=2sinθcosθ=2×$\frac{\sqrt{7}}{4}$×$\frac{3}{4}$=$\frac{3\sqrt{7}}{8}$,
在△ABC中,由正弦定理可得$\frac{AC}{sinB}$=$\frac{AB}{sin2θ}$,
∴AB=$\frac{4×\frac{3\sqrt{7}}{8}}{\frac{\sqrt{3}}{2}}$=$\sqrt{21}$,
故答案为:$\sqrt{21}$.
点评 本题考查了正弦定理和余弦定理和同角的三角函数的关系和二倍角公式,考查了学生的运算能力,属于中档题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.设变量x,y满足约束条件$\left\{\begin{array}{l}x-2y+1≤0\\ x+y-5≤0\\ 4x-2y+1≥0\end{array}\right.$,若目标函数z=mx-y取得最大值的最优解有无数个,则m=( )
| A. | $\frac{1}{2}$ | B. | -1 | C. | 2 | D. | $-1或\frac{1}{2}$ |
6.在2016年巴西里约奥运会期间,6名游泳队员从左至右排成一排合影留念,最左边只能排甲或乙,最右端不能排甲,则不同的排法种数为( )
| A. | 216 | B. | 108 | C. | 432 | D. | 120 |
3.下列函数中,既是偶函数又在(0,+∞)上单调递增的是( )
| A. | y=lgx | B. | y=cosx | C. | y=|x| | D. | y=sinx |