14.若f(x)为奇函数,且x0是y=f(x)-ex的一个零点,则下列函数中,-x0一定是其零点的函数是( )
| A. | y=f(-x)•e-x-1 | B. | y=f(x)•ex+1 | C. | y=f(x)•ex-1 | D. | y=f(-x)•ex+1 |
13.已知向量$\overrightarrow a=(m,2)$,$\overrightarrow b=(2,-1)$,且$\overrightarrow a⊥\overrightarrow b$,则$\frac{|2\overrightarrow a-\overrightarrow b|}{\overrightarrow a•(\overrightarrow a+\overrightarrow b)}$等于( )
| A. | $-\frac{5}{3}$ | B. | 1 | C. | 2 | D. | $\frac{5}{4}$ |
10.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)过点$(\sqrt{2},2\sqrt{2})$,过点(0,-2)的直线l与双曲线C的一条渐进线平行,且这两条平行线间的距离为$\frac{2}{3}$,则双曲线C的实轴长为( )
| A. | 2 | B. | $2\sqrt{2}$ | C. | 4 | D. | $4\sqrt{2}$ |
9.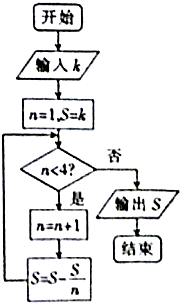 我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )
我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )
 我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )
我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )| A. | 4.5 | B. | 6 | C. | 7.5 | D. | 9 |
5.已知点F2,P分别为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右焦点与右支上的一点,O为坐标原点,若点M是PF2的中点,$|{\overrightarrow{O{F_2}}}|=|{\overrightarrow{{F_2}M}}$|,且$\overrightarrow{O{F_2}}•\overrightarrow{{F_2}M}=\frac{c^2}{2}$,则该双曲线的离心率为( )
0 239131 239139 239145 239149 239155 239157 239161 239167 239169 239175 239181 239185 239187 239191 239197 239199 239205 239209 239211 239215 239217 239221 239223 239225 239226 239227 239229 239230 239231 239233 239235 239239 239241 239245 239247 239251 239257 239259 239265 239269 239271 239275 239281 239287 239289 239295 239299 239301 239307 239311 239317 239325 266669
| A. | $\frac{{\sqrt{3}+1}}{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |