题目内容
11.在△ABC中,a,b,c分别是角A,B,C的对边,△ABC的面积为S,(a2+b2)tanC=8S,且sinAcosB=2cosAsinB,则cosA=$\frac{{\sqrt{30}}}{15}$.分析 由已知利用同角三角函数基本关系式,三角形面积公式,余弦定理化简可得:a2+b2=2c2,利用余弦定理,正弦定理化简sinAcosB=2cosAsinB可得:b2-a2=-$\frac{{c}^{2}}{3}$,联立解得a2=$\frac{7}{6}$c2,b2=$\frac{5}{6}$c2,进而利用余弦定理即可解得cosA的值.
解答 解:∵(a2+b2)tanC=8S,可得:(a2+b2)•$\frac{sinC}{cosC}$=4absinC,
∵C∈(0,π),sinC≠0,
∴a2+b2=4abcosC=4ab•$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=2(a2+b2-c2),整理可得:a2+b2=2c2,①
又∵sinAcosB=2cosAsinB,
∴a•$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=2b•$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$,整理可得:b2-a2=-$\frac{{c}^{2}}{3}$,②
∴联立①②解得:a2=$\frac{7}{6}$c2,b2=$\frac{5}{6}$c2,
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{\frac{5{c}^{2}}{6}+{c}^{2}-\frac{7{c}^{2}}{6}}{2×\sqrt{\frac{5}{6}}c×c}$=$\frac{{\sqrt{30}}}{15}$.
故答案为:$\frac{{\sqrt{30}}}{15}$.
点评 本题主要考查了同角三角函数基本关系式,三角形面积公式,余弦定理,正弦定理在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $2\sqrt{3}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}+1}}{2}$ |
| A. | 2x>2y | B. | lgx>lgy | C. | $\frac{1}{x}>\frac{1}{y}$ | D. | x2>y2 |
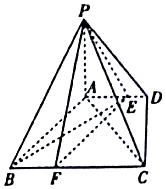 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.